向量绕任意轴旋转的简单推导

数学 - 图形学
, ,

图形学中有关旋转的一个问题是，一个（三维空间的）向量绕一个任意轴旋转若干角度后的角度是什么。本文简单进行推导，给出显式结果。

方法一：向量分解

推导过程

首先介绍一个最容易理解的方法——向量分解。假设要旋转的向量是，要旋转的轴是，是一个单位向量，要旋转的角度是。再设旋转后的轴是。

现在我们把分解为两个向量，一个平行于，另一个垂直于，即： 容易知道，平行于的分向量就是在上的投影（推导过程略）： 从而就能得到： 同样地可以将旋转后的向量分解： 显然，旋转后的向量对应的平行分量是不变的： 这里的关键在于求垂直分量。

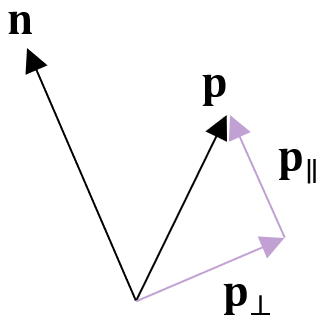
将向量分解为一个平行向量和一个垂直向量

根据已知的旋转轴，我们就知道它对应的平面，而向量与的垂直分量就在该平面内。该平面的维度是2，因此只需要找到两个基向量，就可以通过这两个基向量的线性组合表示该平面的任意向量。

其中一个基向量我们已经找到了，就是，而另一个我们可以通过与的叉乘实现，得到的向量与和垂直，且在平面内。且注意到： 并且有： 进而我们能导出旋转后的垂直分量： 最后，我们得到旋转后的向量：

搞定！

矩阵形式

我们知道向量的叉乘可以表示为： 注意到，矩阵有如下的性质： 所以我们可以把旋转公式写成下述形式： 其中。上面的等式需要注意到。

所以，使用Rodrigues'旋转公式，只需要首先令，然后再计算，就能得到旋转后的向量为。

方法二：坐标轴对齐

既然直接绕着任意轴旋转比较困难，那为啥不先进行整个空间的旋转，把旋转轴旋转为坐标轴，这样就能把向量绕任意轴旋转转化为向量绕标准坐标轴旋转。这就是我们非常熟悉的问题了。

假定我们考虑的是三维空间的旋转（对更高维的情况容易推论），即标准坐标系为。我们有旋转轴和待旋转向量。

首先，我们构建一个坐标系，该坐标系的一个轴就是，我们利用叉乘实现：

现在，我们要把坐标轴分别旋转到坐标轴的位置，这可以用下面的旋转矩阵实现：

很容易验证：，从而就有，这就验证了是正交的。

现在，原来的向量就变成了，原来绕旋转（也就是绕旋转）就变成了绕旋转，而我们知道绕轴旋转的旋转矩阵是： 因此，旋转后的向量就是。现在，只需要把旋转后的向量再旋转回原来的位置就好了，我们只需要再乘以的逆即可。由于是正交的，所以有。把上面的结果合起来，就能得到最终的结果是：

检验

现在我们用代码来检验一下上述三种方法是否能得到同样的结果，以及它们的运算效率如何。比较的方法包括： 1. 向量分解-向量形式 2. 向量分解-矩阵形式 3. 对标轴对齐

程序在虚拟机上运行，RAM为4G，硬盘20G，处理器为2个Intel Core i5-10400F CPU @ 2.90GHz。

代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include<iostream>
#include<eigen3/Eigen/Eigen>
#include<string>
#include<opencv2/opencv.hpp>
#include<chrono>

using namespace std;

const double PI = 3.1415926;

// rotation using vector decomposation - the vector form
void DecomposeVector(const Eigen::Vector3f &n, const Eigen::Vector3f &p, float angle) {
double rotationAngle = angle / 180.0 * PI;

auto startTime = std::chrono::high_resolution_clock::now();

Eigen::Vector3f rotatedVector = cos(rotationAngle) * p 
                                + (1 - cos(rotationAngle)) * (n.dot(p)) * n 
                                + sin(rotationAngle) * (n.cross(p));

auto endTime = std::chrono::high_resolution_clock::now();
double deltaTime = std::chrono::duration<double, std::milli>(endTime-startTime).count();

cout << "Method: vector decomposition - the vector form. The rotated vector p' is (" 
     << rotatedVector(0) << "," << rotatedVector(1) << "," << rotatedVector(2)
     << "). The time used is " << deltaTime << endl;
}

// rotation using vector decomposation - the matrix form
void DecomposeMatrix(const Eigen::Vector3f &n, const Eigen::Vector3f &p, float angle) {
double rotationAngle = angle / 180.0 * PI;

auto startTime = std::chrono::high_resolution_clock::now();

Eigen::Matrix3f N = Eigen::Matrix3f::Identity();
N << 0, -n(2), n(1),
     n(2), 0, -n(0),
     -n(1), n(0), 0;
Eigen::Matrix3f R = Eigen::Matrix3f::Identity() + sin(rotationAngle) * N + (1 - cos(rotationAngle)) * N * N;
Eigen::Vector3f rotatedVector = R * p;

auto endTime = std::chrono::high_resolution_clock::now();
double deltaTime = std::chrono::duration<double, std::milli>(endTime-startTime).count();

cout << "Method: vector decomposition - the matrix form. The rotated vector p' is (" 
     << rotatedVector(0) << "," << rotatedVector(1) << "," << rotatedVector(2)
     << "). The time used is " << deltaTime << endl;
}

// rotation using axis coordination
void AxisCoordination(const Eigen::Vector3f &n, const Eigen::Vector3f &p, float angle) {
double rotationAngle = angle / 180.0 * PI;

auto startTime = std::chrono::high_resolution_clock::now();

Eigen::Vector3f crossed = n.cross(p);
Eigen::Vector3f u = n;
Eigen::Vector3f v = crossed / crossed.norm();
Eigen::Vector3f w = n.cross(v);
Eigen::Matrix3f Q = Eigen::Matrix3f::Identity(), T = Eigen::Matrix3f::Identity();
Q.row(0) = u;
Q.row(1) = v;
Q.row(2) = w;
T << 1, 0, 0,
     0, cos(rotationAngle), -sin(rotationAngle),
     0, sin(rotationAngle), cos(rotationAngle);
Eigen::Vector3f rotatedVector = Q.transpose() * T * Q * p;

auto endTime = std::chrono::high_resolution_clock::now();
double deltaTime = std::chrono::duration<double, std::milli>(endTime-startTime).count();

cout << "Method: axis coordination. The rotated vector p' is (" 
     << rotatedVector(0) << "," << rotatedVector(1) << "," << rotatedVector(2)
     << "). The time used is " << deltaTime << endl;
}

// main
int main()
{
    float angle = 60;
    Eigen::Vector3f p(1.0, 2.0, 3.0);
    Eigen::Vector3f n(2.0, 8.6, -3.1);
    n.normalize(); 
    
    // execute functions
    cout << "The vector p is (" << p(0) << "," << p(1) << "," << p(2) << "). "
         << "The rotation axis n is (" << n(0) << "," << n(1) << "," << n(2) << "). " << endl;
    DecomposeVector(n, p, angle);
    DecomposeMatrix(n, p, angle);
    AxisCoordination(n, p, angle);

    return 0;
}
输出是： 
1
2
3
4
The vector p is (1,2,3). The rotation axis n is (0.213724,0.919011,-0.331271). 
Method: vector decomposition - the vector form. The rotated vector p' is (3.57449,0.643966,0.899062). The time used is 0.016354
Method: vector decomposition - the matrix form. The rotated vector p' is (3.57449,0.643966,0.899062). The time used is 0.016642
Method: axis coordination. The rotated vector p' is (3.57449,0.643966,0.899062). The time used is 0.021062
再多试几组： 
1
2
3
4
The vector p is (1,-654.1,12.88). The rotation axis n is (0.995044,0.0136933,-0.0984901). 
Method: vector decomposition - the vector form. The rotated vector p' is (-59.7309,-338.298,-556.777). The time used is 0.015503
Method: vector decomposition - the matrix form. The rotated vector p' is (-59.7309,-338.298,-556.777). The time used is 0.015297
Method: axis coordination. The rotated vector p' is (-59.7309,-338.298,-556.777). The time used is 0.021547

1
2
3
4
The vector p is (32.5,45.1,-2.2). The rotation axis n is (0.57735,0.57735,0.57735). 
Method: vector decomposition - the vector form. The rotated vector p' is (5.16667,52.4667,17.7667). The time used is 0.015558
Method: vector decomposition - the matrix form. The rotated vector p' is (5.16667,52.4667,17.7667). The time used is 0.015215
Method: axis coordination. The rotated vector p' is (5.16667,52.4667,17.7667). The time used is 0.020841
1
2
3
4
The vector p is (666,0,0). The rotation axis n is (0,0,1). 
Method: vector decomposition - the vector form. The rotated vector p' is (1.78454e-05,666,0). The time used is 0.01517
Method: vector decomposition - the matrix form. The rotated vector p' is (0,666,0). The time used is 0.015402
Method: axis coordination. The rotated vector p' is (1.78454e-05,666,0). The time used is 0.020898

最后一组出现了精度问题，所以代码中还应该加入判断 

1
2
if(abs(value - round(value)) < epsilon)
     value = round(value);

从上面的例子来看，向量分解-向量形式与向量分解-矩阵形式运行效率是一致的，而坐标轴对齐的效率较低，这主要是由计算三次矩阵乘法导致的。