三角形是图形学的基本几何形状，空间中的三角形投射到屏幕空间中为。在内存在一点，它的某个属性常常用三个顶点的属性的插值表示，即重心坐标（Barycentric
coordinates）。然而，在屏幕空间中计算得出的点在三角形内的重心坐标却不一定等于投影前三维空间内对应点在三角形内的重心坐标。这是因为从三维空间到屏幕空间需要执行透视投影（Perspective
Projection），这个投影是非线性的，因此变换前的重心坐标并不能和变换后的重心坐标保持线性关系，从而对三角形顶点的属性插值也不是线性关系。这就需要对透视投影下的重心坐标插值进行修正。本文从透视投影本身出发，说明其非线性性，并根据论文《Perspective-Correct
Interpolation》 给出修正插值。
透视投影的非线性性
三维空间点和向量的表示
图形学一般关心三维空间，或者三维空间中的点。在数学中，既可以表示一个点，也可以表示一个向量，但是在图形学中，我们希望能够将二者区分开来，一个优雅的做法是，增加一个“第四维”，将变为。当时，原来的就表示点，当时，就表示一个向量。这样做的好处是，两个点相减可以正好得到一个向量：
以此类推，向量+点=点（可以理解为某个点沿着向量移动到了另一个点），向量+向量=向量，点+点则无定义。
对点来说，我们可以把每个元素都乘以系数，成为，尽管这时候，但我们依然认为点和点是同一个点，这是因为当把中的每个元素都除以之后，它就是。
这里需要注意的是，“等价”不代表“应然”，在实际使用点的时候（即用点的坐标进行运算的时候），我们仍然要用的版本，也就是，而不是，后者只是为了在一些情况下方便计算。所以在确定好点的空间坐标之后，就要立刻对点进行归一化，把变成1，其他元素都要同样除以。这一点实际上就是透视投影矩阵非线性的根源，下面详细介绍。
透视投影矩阵
（注：以下内容整理、改编自《GAMES101-现代计算机图形学入门-闫令琪》Lecture
4的内容。）
上面我们已经介绍了三维空间中的点，这个点要投影到屏幕空间中形成2D效果，就要经过一系列变换。最简单的变换就是把扔掉，只保留，这个二维向量就是点在屏幕空间中对应的位置。
但是我们人眼在看的时候具有“透视”效果，也就是远处的物体看起来更小，近处的物体看起来更大，而直接用上述做法会让远处的物体和近处的物体看起来一样大。因此在图形学中，我们还需要对点做透视投影，让它呈现出“近大远小”的效果。
如果用一个矩阵表示这个透视投影，那么这个“从三维空间变换为屏幕空间”的过程，就可以描述为：
其中就是我们要求的透视投影矩阵。下面的目标就是如何求出这个矩阵内的元素。
以下图为例。
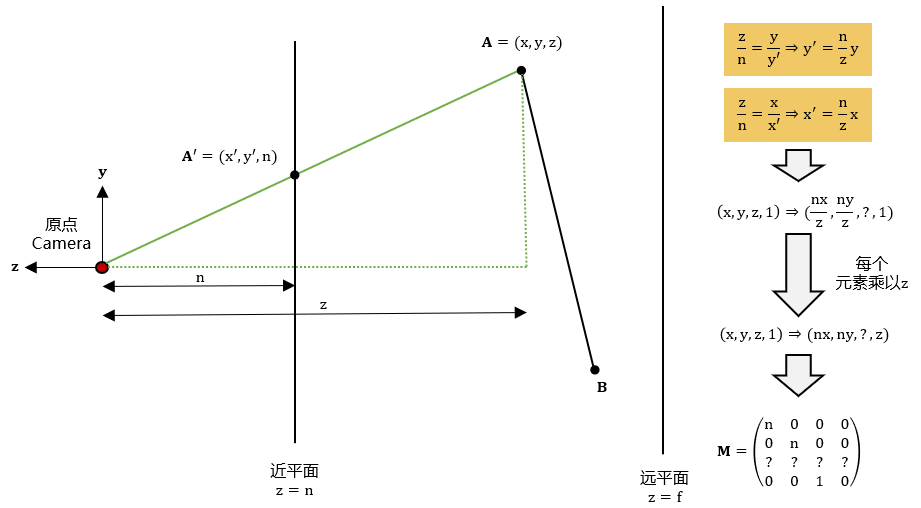三维空间中一个点的x坐标和y坐标满足一定的相似性关系，因此可以直接得出相应的透视投影变换关系。点击图片查看高清原图。
从平面看去，三维空间中的点经过透视投影后的点，在近平面上的位置是屏幕空间（近平面）中的点，这个时候就可以利用相似三角形法则，得到：
同样地，对于平面，也可以得到：
这就是说，透视投影实际上做了下述的变换：
现在把每个元素都乘以，得到。这时候，就有下述方程：
所以可以解得矩阵是：
为什么这里的第三维不是刚才说的近平面呢？这是因为经过透视投影，也就是把点左乘矩阵之后，不一定就是，只是说，我们在保持不变的情况下，把平移到近平面之后，有上述的相似关系。又或者说，当我们从原点往近平面方向看，把近平面当成一个二维空间的时候，在屏幕空间上显示出来的投影后的点是。
比如下面的图二，点经过透视投影之后真正的位置在蓝色虚线上的某一点，它的我们目前是不知道的，但是它的我们可以通过上面的相似关系确定下来。
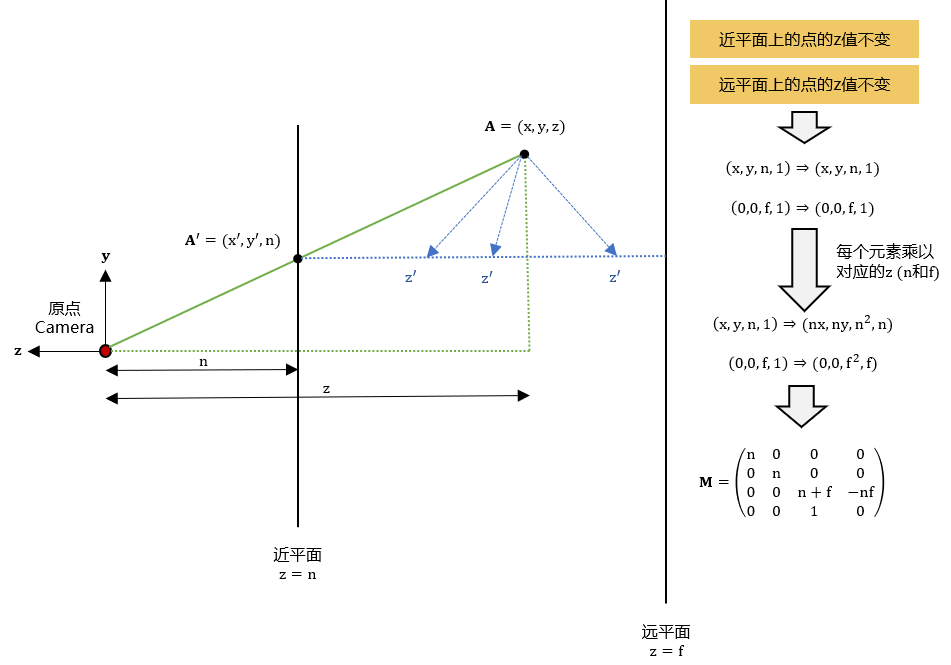三维空间中点，如果它在近平面或者或平面上，则它的z坐标不变。可以利用这个性质解出最终的透视投影矩阵。点击图片查看高清原图。
那么真正的是什么呢？这就要利用透视投影的两个性质：
- 如果一个点在近平面上，那么经过透视投影之后它的位置不变：
- 如果一个点在远平面上，那么经过透视投影之后它的不变：
特殊地，当时有。
如果把矩阵未知的四个量分别设为，那么通过我们有：
因为右式不包含，所以且。
同时，由得到：
与联立求解，就得到。
所以，最终就解得透视投影矩阵为：
这是一个典型的线性变换，把三维空间中的一个点变换到了透视投影之后的某个位置。
现在有个有趣的小问题：透视投影之后的新点（注意不是平移到近平面上的点）的值和原来的相比，谁大？我们只需要计算一下即可：
分子的就是将矩阵的第三行与三维空间中的点点乘后的结果，除以是因为矩阵的实际上是把每个维度都乘了的结果，所以还需要除以还原真实的值（回忆一下我们开始讲的要用真实的值参与计算）。
把乘到右侧之后符号改变，因为这里的坐标轴默认使用的是朝向方向，这可以从上面两个图看出，其中。
解上面的一元二次方程，就得到：
所以，只要当或者的时候，变换后的才比原来的大，然而本身就被限制在了内，所以，透视投影后的永远比变换前的小。换句话说，透视投影把一个点“拉得离屏幕更远”了。
属性插值与透视投影矩阵的非线性性
也许你可能会问了，矩阵不是个线性变换吗，你怎么说透视投影是非线性的。的确，计算出来的矩阵只涉及常数，包括，但是别忘了，它计算出来的结果，是把向量的每一维度都乘以之后得到的结果。真正的经过透视投影后得到的点，还要把每个元素除以才行。正是这个“除以”的操作，决定了整个透视投影是非线性的。
下图是一个例子。三维空间中的线段，经过透视投影之后，在屏幕空间是（始终注意屏幕空间中点的位置和点的真实位置的区别，它们的坐标是不同的）。这时候，直接在屏幕空间中计算重心坐标，得到了点，它正好位于的中间位置，所以，它的属性就应该是和属性的简单平均，也就是。
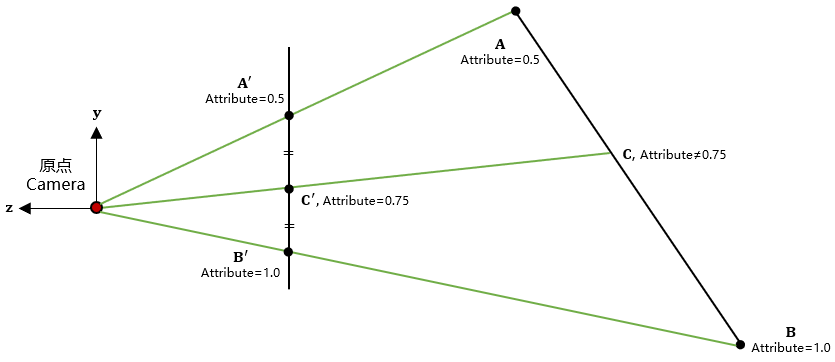屏幕空间的插值不一定与原三维空间的插值保持线性关系。在该图中，A'C'=B'C'，因此C'点的属性就是A'点和B'点的平均，为。但是在原三维空间中，AC的长度不等于BC的长度，因此C点的属性必然不为0.75。然而我们真正关心的是在三维空间中的真实插值，所以需要对屏幕空间中的插值进行修正。
但是，我们真正关心的不是在屏幕空间中插值，而是在透视投影之前，真正的点它位于线段的什么位置，在这个位置的基础上插值，才是点，或者点的属性。这里的属性也包括点的深度值。
从图中可以看到，尽管在屏幕空间中位于的正中间，但是在原来的线段中，点却不是在正中间位置，这正是由透视投影的非线性性导致的，或者说，是由“除以”这个操作导致的。
插值修正
那么点，或者点真正的属性值是多少呢？显然，我们不能再直接用屏幕空间内的插值结果了。
我们以下图为例说明如何对插值进行修正。设屏幕空间的点以及它们中间的某个点，其中离和的距离分别是和。同理，在三维空间的点，以及它们中的某个点。离的距离分别是和。点的属性分别记为和。现在给定和点之外的值，要求出。
进一步，因为我们知道，而又是已知的，所以这里的关键就是求出。
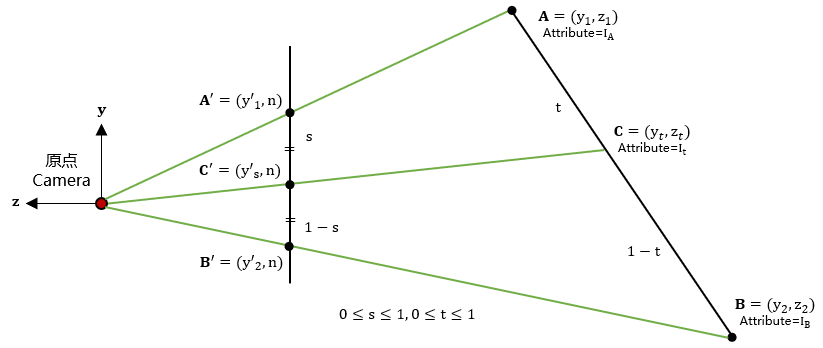设屏幕空间的点以及它们中间的某个点，其中离和的距离分别是和。同理，在三维空间的点，以及它们中的某个点。离的距离分别是和。点的属性分别记为和。现在给定和点之外的值，要求出。
根据上图，我们可以利用相似三角形得到下述三个方程：
同时，根据插值的性质，我们还有下述三个方程：
现在，把公式(4)(5)带入公式(2)中，得到：
再把公式(1)(3)带入公式(7)中，得到：
再把公式(6)带入公式(8)：
把公式(9)化简，就得到了关于的表达式：
式(10)非常重要，它告诉了我们，使用屏幕空间中的插值与三维空间中的深度值可以得到三维空间中的真实插值。
由于深度值本身就是一种属性，所以自然可以使用插值计算。把式(10)带入式(6)，得到：
式(11)告诉我们，三维空间中真实的深度值的计算方法。那么，真实的深度值，也式(11)，和直接在屏幕空间中插值出来的“虚假”的深度值哪个更大？下面直接令:
当或，即点与点或点重合时，真实的深度值和虚假的深度值相等；否则，真实的深度值永远大于虚假的深度值（注意朝向的是方向，因此在把分母乘到右侧的时候需要变号）。换句话说，通过屏幕空间插值出来的深度值，比真实的值要偏小，或更远离屏幕。
为了得到，把式(10)带入到中，就有：
公式(13)就是要求的真实的插值结果。
上面是对线段的插值，那么对图形学中更常见的三角形如何插值呢？假定三维空间中三角形三个顶点的属性分别是，它们的深度值分别是。三角形内有一点，属性值和深度值都未知，但是它在屏幕空间的重心坐标（在屏幕空间中对点的插值）是。那么，根据式(11)，点的真实深度值就是：
再根据式(13)，点的真实属性值是:
这样，就用三维空间中三角形的已知量和屏幕空间的重心坐标求出了点在三维空间中真实的深度值和属性值。
结论
本文从透视投影的概念和推导出发，探究了透视投影的非线性性，进而引出对线段内部和三角形内部点的插值修正。我们真正关心的是在三维空间中对点的插值，而非直接在屏幕空间插值。本文的最后两个公式非常重要，希望读者能够记忆：