1. 1. 复数与二维旋转
    1. 1.1. 定义
    2. 1.2. 复数的加法与乘法
      1. 1.2.1. 复数的加法
      2. 1.2.2. 复数的乘法
    3. 1.3. 复数的模长
    4. 1.4. 复数与二维旋转
      1. 1.4.1. 从复数矩阵形式导出旋转关系
      2. 1.4.2. 复数的极坐标形式
      3. 1.4.3. 复数的几种表示形式总结
    5. 1.5. 旋转复合
  2. 2. 基于Axis Angle的旋转
  3. 3. 欧拉角与万向锁（Gimbal Lock）问题
    1. 3.1. Unity中的Gimbal Lock现象
    2. 3.2. 欧拉角、坐标系与旋转顺序
    3. 3.3. Unity中的欧拉角
    4. 3.4. Unity中的Gimbal Lock问题
  4. 4. 四元数
    1. 4.1. 定义
    2. 4.2. 加法、乘法、模长
      1. 4.2.1. 加法
      2. 4.2.2. 乘法
      3. 4.2.3. Graßmann积
      4. 4.2.4. 模长
    3. 4.3. 纯四元数
    4. 4.4. 共轭
    5. 4.5. 逆
  5. 5. 四元数与三维旋转
    1. 5.1. 从三维旋转公式到四元数表示
    2. 5.2. 四元数旋转公式的简化
      1. 5.2.1. 引理一
      2. 5.2.2. 引理二
      3. 5.2.3. 引理三
    3. 5.3. 三维旋转定理（四元数型）
    4. 5.4. 四元数乘积的性质
    5. 5.5. 三维旋转定理（矩阵型）
    6. 5.6. 三维旋转定理（指数型）
    7. 5.7. 旋转复合
    8. 5.8. 双倍覆盖
  6. 6. 四元数插值
    1. 6.1. 基于幂运算的插值
    2. 6.2. 四元数在四维空间内的夹角
    3. 6.3. Lerp, Nlerp, Slerp
      1. 6.3.1. Lerp
      2. 6.3.2. Nlerp
      3. 6.3.3. Slerp
    4. 6.4. 双倍覆盖问题
  7. 7. Squad
    1. 7.1. Bézier曲线
    2. 7.2. 三次Bézier曲线
    3. 7.3. de Casteljau算法
    4. 7.4. Squad
    5. 7.5. Squad应用
  8. 8. Angle、Euler、Matrix、Quaternion之间的相互转换
    1. 8.1. Angle转化为其他形式
      1. 8.1.1. Angle转化为Euler
      2. 8.1.2. Angle转化为Matrix
      3. 8.1.3. Angle转化为Quaternion
    2. 8.2. Euler转化为其他形式
      1. 8.2.1. Euler转化为Angle
      2. 8.2.2. Euler转化为Matrix
      3. 8.2.3. Euler转化为Quaternion
    3. 8.3. Matrix转化为其他形式
      1. 8.3.1. Matrix转化为Angle
      2. 8.3.2. Matrix转化为Euler
      3. 8.3.3. Matrix转化为Quaternion
    4. 8.4. Quaternion转化为其他形式
      1. 8.4.1. Quaternion转化为Angle
      2. 8.4.2. Quaternion转化为Euler
      3. 8.4.3. Quaternion转化为Matrix

四元数与旋转

数学 - 图形学
, , , ,

图形学中的旋转（Rotation）非常重要，用欧拉角（Euler Angle）旋转非常简单，但是却存在 万向锁（Gimbal Lock） 的问题；同时，用欧拉角插值也不尽方便。基于四元数（Quaternion）的旋转既解决了万向锁的问题，又能非常便利地插值。本文将从概念出发，对四元数的定义、推导、性质、应用，以及它与欧拉角之间的联系进行介绍。本文主要参考了Krasjet的《四元数与三维旋转》1，其他参考内容包括2345678。

复数与二维旋转

首先我们将简要介绍复数及它与二维旋转的关系，从而可以更加自然地过度到四元数及其与三维旋转的关系。

定义

复空间中的任一复数都可以表示为的形式，且满足。此时称为复数的实部 (Real Part)，表达为；称为复数的虚部 (Imaginary Part)，表达为。

从线性代数的角度来看，复数可以看成是基 (Basis) 上的线性组合，因此也可以把复数写成一个向量：

复数的加法与乘法

复数的加法

复数的加法很简单，分别把实部和虚部相加即可。减法类似，不多赘述。

复数的乘法

对复数，它们相乘的结果为：

利用上面讲过的复数的向量形式，可以把上式写成矩阵乘向量的形式：

右侧的向量就是向量形式下的，而左侧的矩阵则是在乘法时的矩阵形式，矩阵的第一列就是自身的向量形式，而第二列进行了交换并对虚部取负。

所以，我们可以把也写成矩阵形式，然后与相乘：

所以，我们现在可以用至少三种形式去表达一个复数了（具体用哪种形式取决于我们的需要）：

  • 代数形式：;
  • 向量形式：;
  • 矩阵形式：.

有两个特殊的复数，它们的矩阵形式不难得到是：

对复数的矩阵形式进行平方，发现它就是，从代数形式来看，就等价于。这说明复数的矩阵形式是良定义的。

复数的模长

复数的模长（Magnitude）定义为:

这可以用它的共轭（Conjugate）表示：

复数与二维旋转

从复数矩阵形式导出旋转关系

下面将重点引出复数与二维旋转的关系。

注意观察复数的矩阵形式，我们可以把它变换为下述形式：

矩阵中的每一项都被模长缩放了，此时注意到就是复数在复平面与实轴形成夹角的余弦值，而正好对应了正弦值，而这个夹角就是。

这样一来，我们就可以把上式写成：

这样一来，任意复数都可以表示为两个矩阵的乘积，一个缩放矩阵和一个（我们熟悉的）旋转矩阵的复合。换句话说，复数的几何意义就是进行旋转与缩放，旋转角度为，缩放大小为复数的模长。 如果复数的模长为1，那么它的几何意义就只有旋转。

所以，对复数的旋转：

我们可以构造一个复数，把它与相乘表示旋转：

复数的极坐标形式

当我们看到式的时候，我们立马可以得到复数的另一种代数形式：

再根据欧拉公式（Euler's Formula）：

可以立得复数的极坐标形式：

现在，复数不再通过它的实部和虚部表示，而且通过一个旋转角与缩放因子去表示了，它对任意一个复数的旋转，都可以表示为：

如果仅需表示旋转，则令即可。

Proof of Euler's Formula：
令，对实数，对求导，得到，因此是常数。又因为，所以。欧拉公式得证。

复数的几种表示形式总结

现在我们已经得到了如下几种复数的表示形式：

  • 代数形式一：;
  • 向量形式：;
  • 矩阵形式一：;
  • 矩阵形式二：;
  • 代数形式二：;
  • 极坐标形式：.

这几种形式是完全等价的。

旋转复合

假设我们现在有两个仅表示旋转的复数，相继用它们对一个复数旋转：

所以，用两个复数进行旋转时，所得到的结果仍然是一个旋转，且旋转的角度是两次旋转角度之和。

基于Axis Angle的旋转

在这篇博客中，我们已经介绍了三维空间中一个向量绕任意轴旋转的公式（被称为Rodrigues' formula）。因为下文会涉及大量此公式，因此把结论在此重新记述，推导过程请参考原文。

记是待旋转的向量，是被围绕旋转的轴，是一个单位向量，是要旋转的角度，是旋转后的向量。我们有：

或者矩阵形式：

因为这种旋转方式是通过一个旋转轴和一个旋转角度定义的，所以我们称之为Axis Angle旋转。 请记住此公式，我们将看到它与四元数之间紧密的联系。

欧拉角与万向锁（Gimbal Lock）问题

Unity中的Gimbal Lock现象

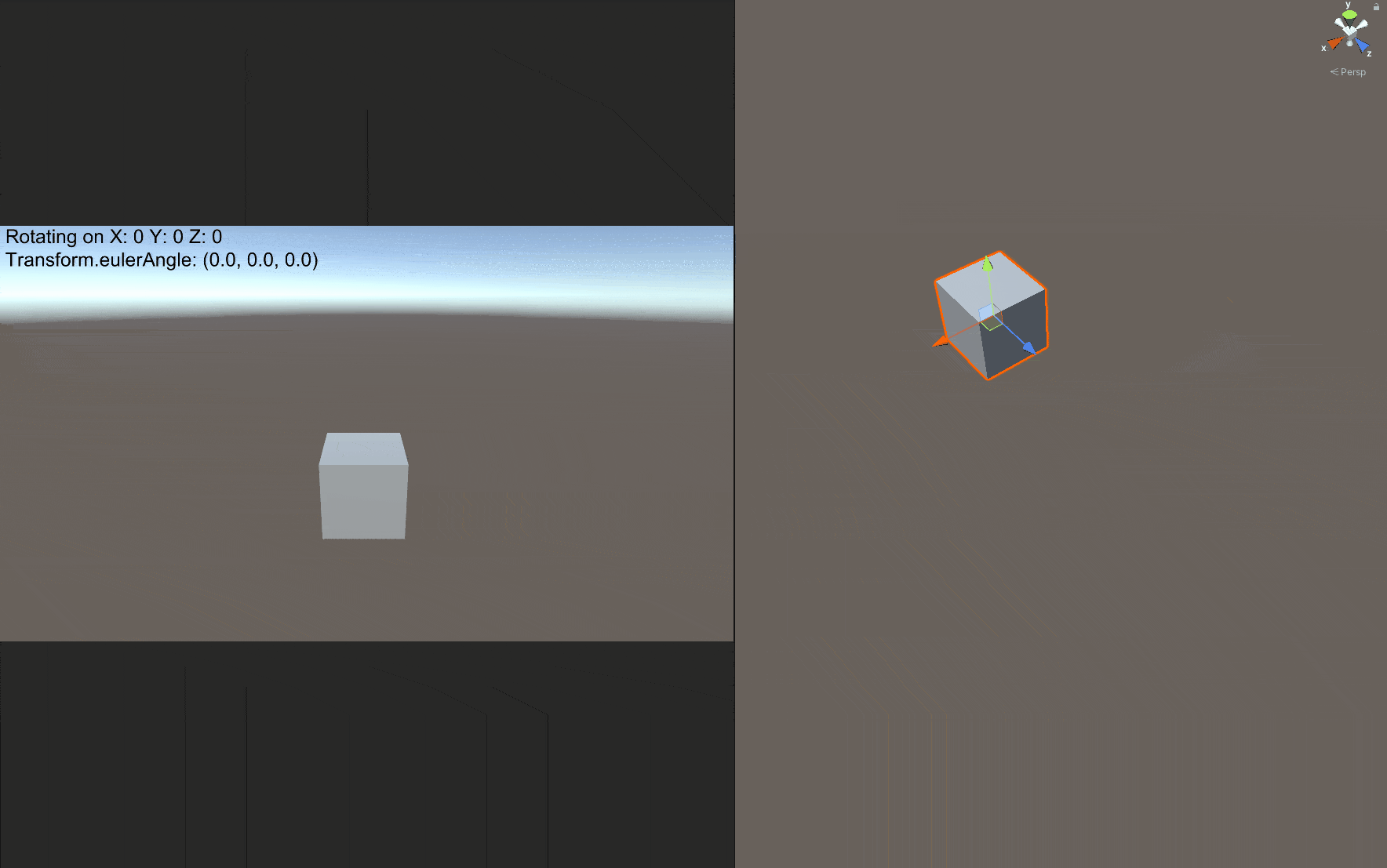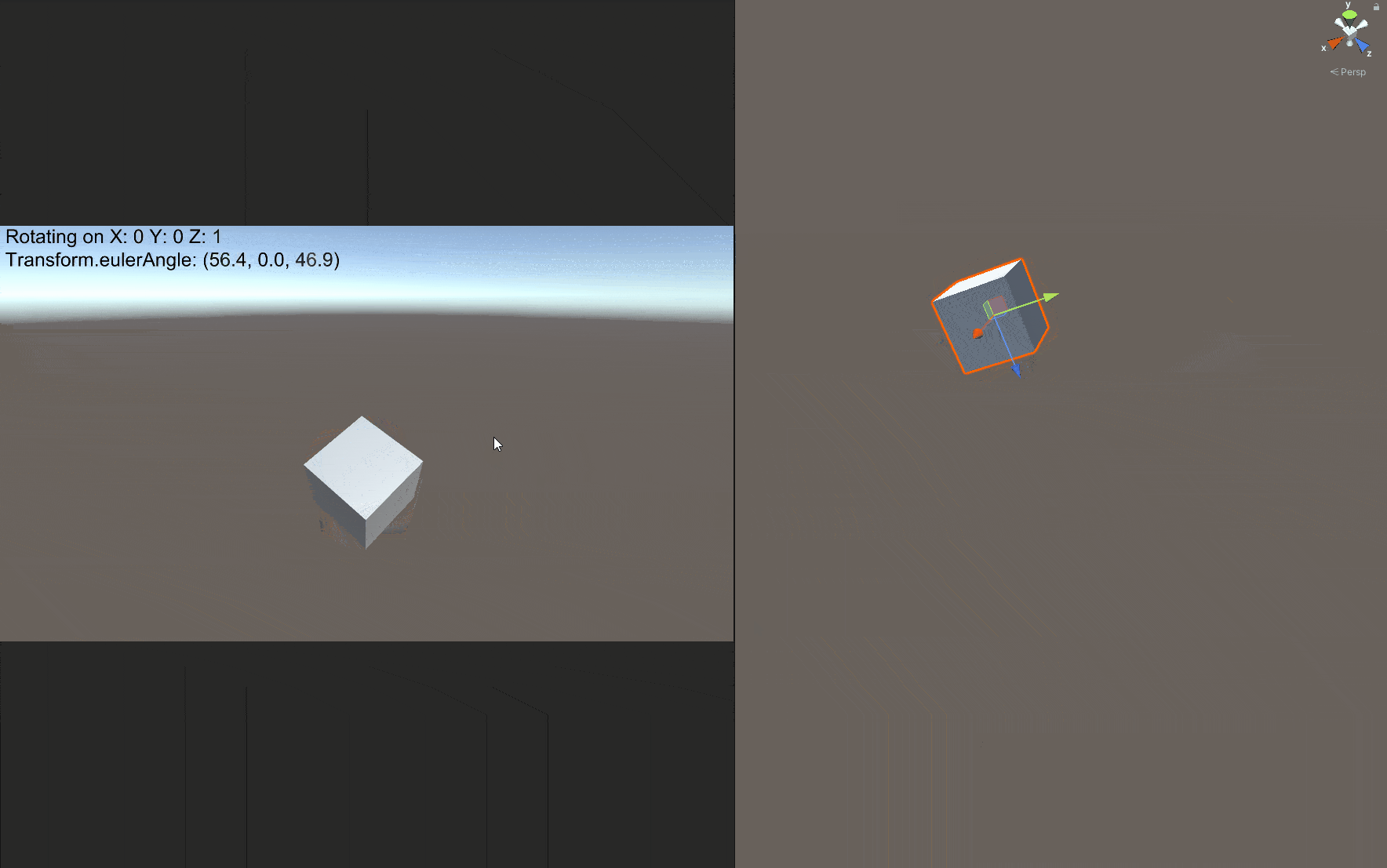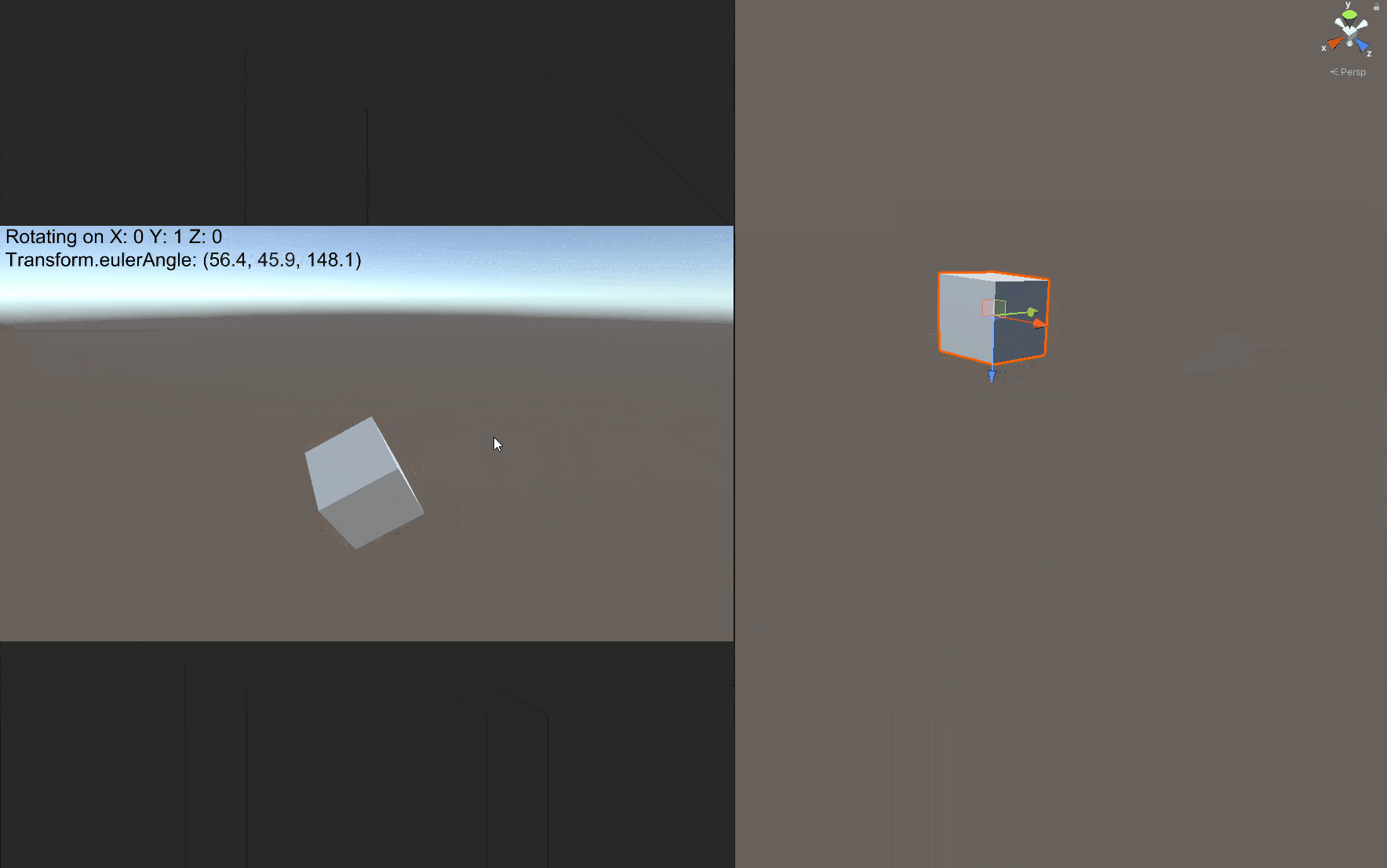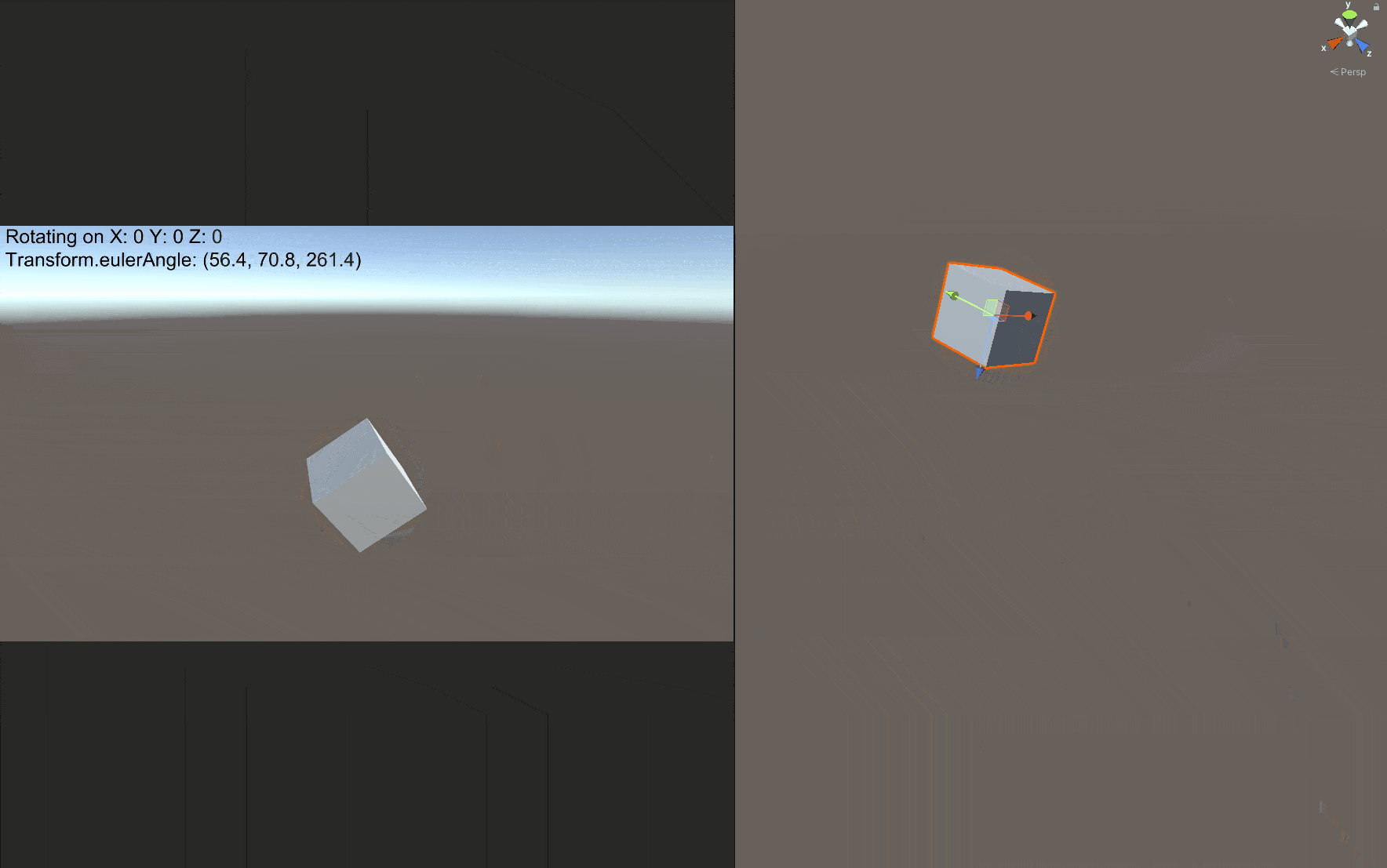
在正式进入四元数之前，我们先介绍欧拉角及其引发的万向锁问题。网上有很多关于Gimbal Lock的文章，但是找了一通发现大都表述得非常抽象。下面我把这个现象放到Unity中可视化展示，读者应该就能立刻知道问题所在。

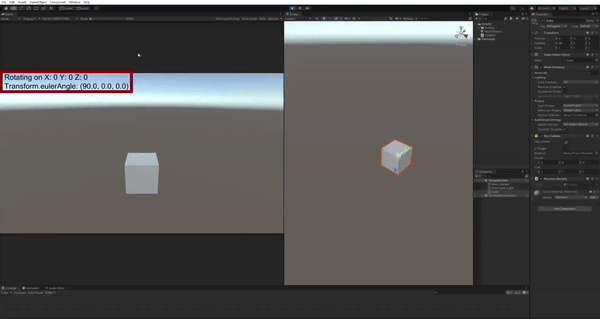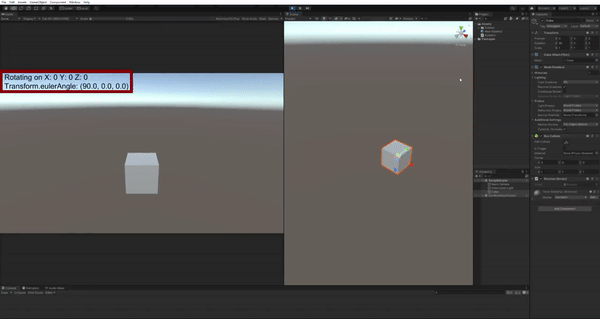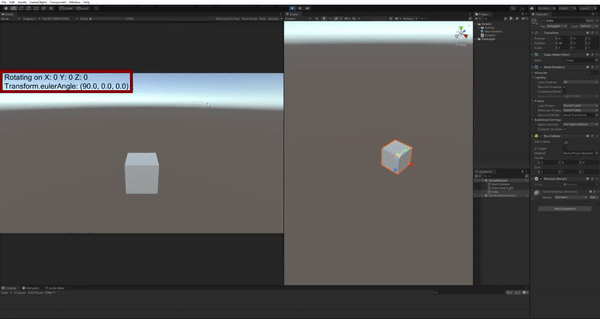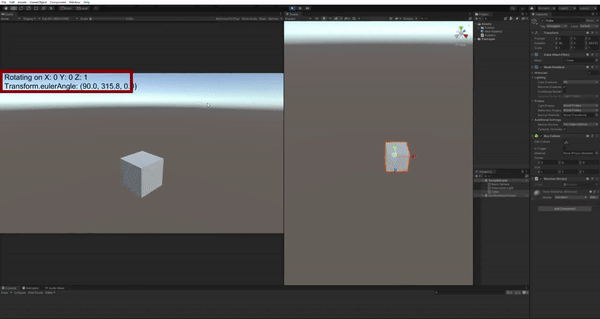
注意左上角红框圈出的部分，X/Y/Z=1表示这个Cube正在绕世界坐标系的x/y/z轴旋转，在我们一开始就把Cube绕x轴旋转90度时，我们惊异地发现，旋转y轴或者z轴的效果都是一样的！显然这不是我们想要的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Rotation : MonoBehaviour
{
    float rotationSpeed = 45;
    Vector3 currentEulgerAngles = new Vector3 (90, 0, 0); // Rotating 90 degree
    float x, y, z;

    void Update()
    {
        if (Input.GetKeyDown (KeyCode.X)) x = 1 - x;
        if (Input.GetKeyDown (KeyCode.Y)) y = 1 - y;
        if (Input.GetKeyDown (KeyCode.Z)) z = 1 - z;

        currentEulgerAngles += new Vector3 (x, y, z) * Time.deltaTime * rotationSpeed;

        transform.eulerAngles = currentEulgerAngles;
    }

    void OnGUI ()
    {
        GUIStyle style = new GUIStyle ();
        style.fontSize = 24;

        GUI.Label (new Rect (0, 0, 0, 0), "Rotating on X: " + x + " Y: " + y + " Z: " + z, style);
        GUI.Label (new Rect (10, 25, 0, 0), "Transform.eulerAngle: " + transform.eulerAngles, style);
    }
}

那么为什么会出现Gimbal Lock现象呢？核心原因在于欧拉角旋转顺序是被固定的。要理解这句话，我们就要首先知道什么是欧拉角，什么叫固定顺序旋转。

欧拉角、坐标系与旋转顺序

如果你没有任何基础知识取看Wikipedia的Euler Angles页面，你一定会感到一脸懵逼。从严格的定义来看，Wikipedia的介绍比较准确，但是在这里我们只需要简单地把欧拉角理解为点绕着世界坐标轴旋转的角度即可。

欧拉证明了三维空间中的任意旋转都可以拆分为沿着自身的三个坐标轴的旋转，欧拉角就是这三次旋转的角度。但是在这里我们使用相对于世界坐标系的旋转角度，这是因为相对自身坐标系的旋转与相对世界坐标系的旋转是可以互相转换的，只需要把旋转矩阵按照相反顺序相乘即可。

我们把绕着自身坐标系旋转称为intrinsic rotation，把绕着世界坐标系旋转称为extrinsic rotation。

假定点绕世界坐标轴分别旋转度，则旋转后的位置等价于绕自身坐标轴分别旋转度。

证明：

我们知道在世界坐标系中绕轴旋转的旋转矩阵分别为：

用的顺序进行旋转，得到复合旋转矩阵：

现在考虑在点的局部坐标系上按照的顺序旋转，注意，因为是局部坐标系，所以每次旋转都会同等地旋转每个局部坐标轴。旋转之前的局部坐标系与世界坐标系重合。我们能够得到上述绕自身局部坐标系旋转的旋转矩阵：

这里要稍微做一些解释。粉色的就是最开始基于轴的变换，在这个变换之后，局部坐标系也跟着进行了变换，如下图所示：

可以看到在绕轴旋转的过程中，自身局部的轴也在随之旋转。接下来我们想要绕着自身的轴旋转，我们先看看直接操作旋转是怎样的效果：

可以看到上图进行了两次旋转操作，第一次是绕着自身（其实也是世界坐标系）的轴旋转了约度，第二次是绕着自身的轴（绿色轴）旋转了约度，得到了一个倾斜的正方体。

那么，绕自身轴旋转这个过程该怎么用数学形式表示呢？其实我们可以这么想：无论局部坐标系怎么变，绕自身的轴旋转这个操作都是相对不变的，也就是说，无论有没有第一步的绕轴旋转，绕轴旋转前后所得到的位置相对自身坐标系而言都是相同的。如此一来，我们就可以先把绕轴旋转这个操作还原回去，进行绕轴旋转的操作，然后再恢复到绕轴旋转后的状态，这样就求出了我们原本期望的旋转，也就是绿色部分进行的操作。

这个过程可以用下图表示：

首先我们绕轴旋转了度，然后又还原了回去绕轴旋转度，最后再恢复到第一步操作后的状态。这里要特别注意的是，最后"恢复到初始状态"这个操作，是针对世界坐标系而言的，而不是当前的局部坐标系，这是因为我们第一步绕轴旋转度本质上就是在世界坐标系中进行的。

如果你还不理解，我们再来看一下最后公式的粉色部分，这里的就是前两步旋转的结果，而就是对这个旋转整体取反向操作，回复到最开始的没有旋转的状态。所以这时候你应该明白，应该把看作一个整体，而这个整体表示的旋转就是相对于世界坐标系而言的。无论之后是否还有更多的旋转，都可以采用这种思路套娃下去。

有了上述结论，我们在这里就不再关心是局部坐标系还是全局坐标系了，我们默认使用全局坐标系。

此外，顺序对基于欧拉角的旋转来说至关重要，这是因为矩阵往往不具备交换律，即。所以在实际应用的时候，我们会固定采用一个顺序进行旋转，比如。这种按照固定顺序旋转的做法就导致了Gimbal Lock的产生。

Unity中的欧拉角

Unity中的欧拉角是采用的顺序进行旋转的。采用顺序旋转的直接结果是：当我们固定了和轴旋转后再增量基于轴旋转，会发现物体是在绕着自身的轴旋转而不是绕着世界坐标系的轴旋转。如下图所示：

这是因为当我们变动欧拉角的时候，Unity会重新按照的顺序计算旋转。如果我们固定了轴和轴的旋转角，不断地变动轴旋转角的时候，Unity会首先对轴进行旋转，然后才是对和轴，然而在对轴旋转的过程中，物体的局部坐标系也在随之变动。既然我们已经固定了轴的旋转角度，变换的只有轴，所以最终呈现出来就是物体在绕自身局部坐标系的轴旋转。

Unity中的Gimbal Lock问题

有了上面的铺垫，我们就知道为什么会出现开头那样的Gimbal Lock现象了。当我们固定轴的旋转角度为度时，再设绕轴和轴的旋转角度为，我们可以把以为顺序的复合旋转矩阵写为：

我们发现，这个旋转矩阵竟然仅仅是旋转了和轴，它并没有对物体本身的轴做旋转（可以看本节最开始的视频，正方体围绕蓝色的轴，也即自身的轴在旋转），而是把两个变换合并为了一个变换。还记得我们上一小节讲到的固定轴只变动轴时物体围绕自身的轴旋转的现象吗？在这个地方，我们固定了轴的旋转为度，对轴和对轴的变换都作用到了轴上，所以最终呈现的效果就是物体绕了轴旋转度之后只能围绕自身的轴旋转。我们再也没有机会对物体原本的轴进行变换了，这就是所谓的Gimbal Lock问题。

所以，由此可见，Gimbal Lock产生的根本原因在于采用固定的旋转顺序，因为旋转顺序固定，所以就会在某些情况（如此处轴恒定旋转为度）下失去一个轴的自由度。采用欧拉角就意味着旋转顺序有先后，就必然会出现Gimbal Lock问题。

除了Gimbal Lock之外，Euler Angles还存在插值困难和歧义性（与旋转矩阵之间的对应关系复杂）等问题。

四元数

定义

四元数可以定义为如下形式：

这个定义和复数非常相似，只不过四元数有三个“虚部” ()，而复数只有一个“虚部” ()。

上述的满足如下性质：

如果把上式称为四元数的代数形式，那么同样地，它也可以有对应的向量形式一：

如果把四元数的“实部”和“虚部”拆开，那么四元数还可以表示为下述的向量形式二：

所以，仅仅从定义来看，四元数就有如下三种等价的形式：

  • 代数形式：;
  • 向量形式一：;
  • 向量形式二：.

加法、乘法、模长

加法

给定两个四元数与，定义四元数的加法为：

用四元数的向量形式，可以把上式简化为：

乘法

四元数的标量乘法和实数、复数一样，可以定义为：

然而四元数之间的乘积可以通过如下步骤定义：

我们可以从性质推导出如下的性质：

, , , , ,

于是能够得到下表：

容易观察到交换律并不成立，即。利用这个表格，我们能够对四元数之间的乘法进行归纳简化：

现在，得到的这个新四元数的四个分量都表示了出来，即：

或者可以写成下述的矩阵形式：

这样一来，我们就把两个四元数的乘积写成了矩阵与向量的乘积，并且由于四元数的乘法不可交换，代表的仅仅是为左乘数、为右乘数时的结果。我们把矩阵称为四元数当右乘子时的变换矩阵，或矩阵形式。

Graßmann积

显然矩阵形式又臭又长，我们希望用一种更简单的形式——Graßmann积——去表示四元数乘法。

重新整理之前的乘法结果：

如果令，则有：

这样一来，我们就可以用点乘和叉乘的形式表示四元数的乘积：

这就是所谓的Graßmann积（Graßmann Product）。所以，从Graßmann积也可能看到两个四元数的乘积一般是不可交换的，因为叉乘一般不可交换。

模长

四元数的模长和向量的模长定义一样：

纯四元数

定义“实部”为零的四元数为纯四元数，即：

对于两个纯四元数，它们的乘积为：

共轭

四元数的共轭（Conjugation）与复数的共轭类似，可以定义为：

四元数与它自己的共轭相乘可以得到一个标量：

正好是四元数模长的平方。同时：

这表明四元数与它共轭的乘法是可交换的。这是一个非常好的性质。

逆

有了共轭，我们最后就可以来定义四元数的逆（Inverse）了。记四元数的逆为，则是满足下述性质的四元数：

利用共轭，我们可以进行如下推导：

所以，四元数的逆就是它的共轭除以它模长的平方。如果，那么它的逆就是它的共轭，此时称为一个单位四元数 (Unit Quaternion)。

四元数与三维旋转

从三维旋转公式到四元数表示

现在我们正式考察四元数与三维旋转之间的关系。首先，让我们回忆一下普通3D旋转的推导过程：

A sketch derivation of Rodrigues' formula：
记是待旋转的向量，是被围绕旋转的轴，是一个单位向量，是要旋转的角度，是旋转后的向量。则：

现在我们想要找到四元数与上式的关系，我们自然地想到能不能像推导四元数乘法的矩阵形式那样，把上面所有的向量都用四元数去表示。于是我们可以定义：

从而我们有：

前面两项我们已经顺利地用四元数表示出来了，但是第三项的叉乘怎么办？我们先尝试一下用对应的四元数相乘看看：

这里就用到了纯四元数的概念。不管怎样，我们很“幸运”地用四元数的乘法把最后的叉乘表示了出来，代入中，就有：

这里的用四元数的向量就可以表示为，而且还可以验证它是一个单位四元数（模长为1）！

四元数旋转公式的简化

现在我们也可以像之前那样，分别把代入，但是我们想要更好的形式。为了进一步化简上式，我们需要证明三个引理。

引理一

如果，且为单位向量，则.

证明从略。

现在我们引入一个新的四元数，根据引理一，我们显然有，并且也是单位四元数，从而。

所以，之前的结果现在就可以重写为：

这里用的原因就是要把两项都表示为三个因子的乘积。实际上是一个恒等变换，它并不对产生作用，真正起作用的是，它对旋转了度，使得相加后能得到正确的结果。

但是这种形式还是不能简化右式，我们需要下面的引理二。

引理二

如果是一个纯四元数，，其中是单位向量，。若平行于，则.

该引理证明如下：

根据引理二，我们就可以把上式的第一项最后两个因子交换，得到：

我们再使用引理三进行最后的化简。

引理三

如果是一个纯四元数，，其中是单位向量，。若正交于，则.

证明与引理二过程类似，不多赘述。根据这个引理，我们就能对原式做最后的化简：

最后我们得到了一个非常优美的结果，在这个公式中，我们不再把待旋转向量拆分为两个分量，而是直接通过四元数之间的乘法实现了旋转。该结论可以总结为一个定理：

三维旋转定理（四元数型）

3D Rotation Theorem (Quaternion)： 任意三维向量绕着单位向量旋转度之后的向量可以用下式表示：

现在我们进行验证：

正好就是Rodrigues' formula！

并且，从上面的推导我们还知道：所有的单位四元数都对应了一个三维旋转（但这二者之间并非双射）。那么给定单位四元数，我们就能得到它对应的旋转角和旋转轴：

因此，我们得到了：

四元数乘积的性质

下面我们介绍几个关于四元数乘积的性质，这些性质与我们的主题没有直接关联，但对我们深入理解四元数大有帮助，供感兴趣的读者参考。

Property 1：
令为单位四元数，，则满足且。

证明：

此外，还有，从而推得。

Property 1告诉我们：对四元数的旋转不改变标量和向量的模长。这与四元数表示旋转的本质是符合的。

Property 2：
令都为单位四元数，，对有。

证明：

其中第四个等号和第七个等号可以通过Property 1推知。

Property 2告诉我们：对一个单位四元数的次幂旋转，等价于对单位四元数旋转的次幂。

接下来的四个性质与单位四元数的求导有关。

Property 3 (Derivative of exponential)：
令为单位四元数，，则有：

证明：

Property 4 (Product rule)： 设是将实数映射为四元数的连续函数，从而有：

证明：

Property 5 (Chain rule)： 设是将四元数映射为四元数的连续函数，是将实数映射为四元数的连续函数，则有：

证明：

Property 6： 设是将实数映射为四元数的连续函数，是将实数映射到实数的连续函数，再设。我们有：

证明：

最后一个Property联系了四元数的乘积与点乘。

Property 7： 设是三个四元数，则有。

证明：

使用恒等式，我们有：

最后，我们使用下述等式：

现在我们有：

三维旋转定理（矩阵型）

通过之前的讨论（尽管不完全相同，但可以类似推导）我们知道左乘一个四元数等同于下面的矩阵

而右乘等同于

现在我们就可以利用这个结论把写成矩阵形式。假定，我们就有：

实际上我们不需要存这个完整的的矩阵，只需要存右下角的矩阵即可。如此一来，我们就得到旋转定理的矩阵形式：

3D Rotation Theorem (Matrix)：
任意三维向量绕着单位向量旋转度之后的向量可以用下面的矩阵表示：

其中.

尽管看起来比较复杂，但是在实际中如果旋转轴和旋转角度固定了之后，该矩阵就可以预先计算下来，在需要旋转很多时提高效率。

三维旋转定理（指数型）

类似复数，我们也可以把四元数写成指数的形式。如果是一个单位向量，对于单位四元数，我们有:

也就是说，可以写为。你还可以注意到，这与复数中的是非常类似的。

3D Rotation Theorem (Exponential)：
任意三维向量绕着单位向量旋转度之后的向量可以用下面的指数表示：

其中.

有了指数形式，我们就可以很自然地运用关于指数的一些运算了。比如对单位四元数，的对数是：

下面是幂运算；

即一个单位四元数的次幂等同于旋转角缩放到原来的倍，且不会改变旋转轴。

旋转复合

现在来考虑基于四元数的旋转复合，假设分别在四元数上进行旋转，则有：

上式隐含了，它的证明不多赘述。

需要注意的是，复合后旋转是绕着一个新的旋转轴旋转某个角度，尽管结果是相同的，但是过程完全不同。

双倍覆盖

单位四元数与三维旋转并不是双射（一对一）的，一个单位四元数对应一个三维旋转，但是一个三维旋转可以找到两个单位四元数去对应它，这就是所谓的2对1满射同态，或者说单位四元数双倍覆盖了三维旋转。

具体来说，与代表了同一个旋转：

即是绕着轴旋转了度，正好是代表的旋转。这个结果也可以从四元数旋转公式得到：

现在我们已经知道四元数相比欧拉角而言的优点了：

  • 插值非常简单（将在下一节介绍）；
  • 几何意义明显，双倍覆盖三维旋转；
  • 与旋转的顺序无关，一次四元数乘法即可完成旋转；
  • 约束少，仅要求为单位四元数；
  • 不存在Gimbal lock；
  • 复合旋转简单。

四元数插值

基于幂运算的插值

假设有两个旋转变换，我们希望能够通过得到它们的中间旋转变换。

然而直接求这个中间旋转似乎比较困难，我们不妨从结果出发，期望原始向量在经过旋转之后得到的向量，它能够位于和之间。所以，对于向量而言，它是先变换到，再进行的变换到。特殊地，当的时候，就变换到了的位置，这可以表示为：

根据旋转定理的指数型，我们只要对取次方，就能得到插值对应的旋转了。所以：

这个插值方法称为Slerp，但它涉及到多个四元数的乘法，而且还包含幂运算，实际应用中效率很低。我们一般的插值都是使用线性组合，而不是幂运算。

四元数在四维空间内的夹角

公式低效的根本原因在于我们把插值旋转直接用的乘积表示出来了，但我们真正关心的是对角度和旋转轴进行插值。为此，我们需要首先研究下公式如何表示旋转角的。

我们有；

如果我们把看作两个四维向量，我们发现，的实部正好就是点乘的结果。同时，又因为是两个单位向量，所以它们点乘的结果就是它们夹角的余弦，记为。所以我们有。

与此同时，我们又知道也代表的是一个旋转，记旋转角为，它的实部为，从而有。在区间上当且只有一个解。这也就意味着，在四维空间中的夹角，正好是它们作为四元数时旋转变化量所代表旋转角度的一半，即。基于这个事实，我们套用向量的插值公式对四元数进行插值。

Lerp, Nlerp, Slerp

前文已经提到，我们希望对四元数进行线性插值，即表示为的形式。下面介绍三种线性插值方法。

Lerp

第一种是我们熟知的线性插值Lerp：

但是，这种插值方法得到的四元数并不是单位四元数，也就是并不能真正表示三维旋转。现在我们来验证一下：

显然，当时，上式不等于1，这也就意味着Lerp插值的结果并不是一个单位四元数。

Nlerp

既然Lerp的结果不是一个单位四元数，那么除以它的模长不就可以变成单位四元数了吗？这就是所谓的Nlerp（Normalized Lerp）：

但是Nlerp的问题在于，随着的增大，的旋转角变化幅度会发生变化，或者说，的旋转角变化不是线性的。

如下图所示，从变换到与从变化到旋转角的变化幅度不一样；同样地，从到与从到旋转角的变化幅度也不一样。我们希望能够线性地改变旋转角。

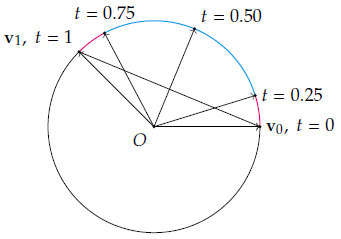
Slerp

所以，我们想要直接对角度插值。如果之间的夹角为0，那么：

因为对角度线性插值相当于是让向量在球面上的一个弧上旋转，所以这种插值被称为球面线性插值Slerp（Spherical Lerp）。我们最开始说到的基于幂运算的插值就是我们接下来要介绍的Slerp的一种等价形式。

对于向量，我们希望能够直接表示为二者的线性组合：

为了求解，我们对上式两边同乘（设之间的夹角为）：

同样地，对两边同乘：

现在，把代入上式，我们就有：

把代回去，就能解得：

于是，我们能就得到最终Slerp的公式：

现在的Slerp已经比最开始介绍的基于幂运算的Slerp快很多，但是由于它涉及了三个三角函数、一个反三角函数和一次点乘，所以效率仍然比Nlerp低一些。此外，如果夹角很小，可能因浮点精度问题被近似为，导致运算错误。所以在实际使用Slerp时，要首先判断夹角是否较小，若是，则改用Nlerp，而由于夹角很小，Nlerp与Slerp的误差可以忽略。

需要注意的是，Slerp并不是一个“万能答案”，它的运行效率显著低于Nlerp。此外，Nlerp的角速度变化不一致并不一定是个坏处，在不同的情景下可能有不同的用处。所以，在使用插值方法的时候要根据实际情况选择，大多数时候Nlerp已经足够了。

双倍覆盖问题

之前我们介绍过，四元数与代表的是同一个旋转，这就导致对两个四元数的插值会有效率差距。

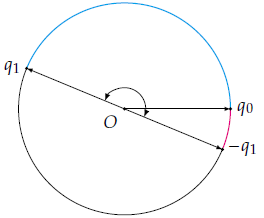
如下图所示，虽然可以从到方向插值，但是由于与代表的是同一个旋转，而与的夹角更小，插值造成的误差更小，所以我们这时会选择从插值到。

这告诉我们，在对四元数插值之前，要检查之间的夹角是否是钝角，即检查它们的点积结果是否是负数，如果是负数，就对其中一个四元数取负号，然后在新的四元数间插值。

Squad

Slerp已经是我们理想中的插值方式了：它直接对角度插值，插值角度匀速变化，运算效率尚可。但是它还有一个小问题：角度变化的速率等于夹角，即，这就意味着，当我们在多个角速度之间插值的时候，当在不同的四元数之间插值的时候，速率会发生突变，或者说在切断点处不可导。从数学上讲，函数连续并不意味着函数的一阶导连续（前者称为连续，后者称为连续）。

为此，我们希望插值的曲线能够在高阶导处也连续，下面介绍的Squad（Spherical and quadrangle）就是一种解决方法。

下图是Slerp和Squad的插值结果比较，曲线是每个四元数插值结果的角速度。可以看到：Slerp在四元数切换时角速度会发生突变，而Squad的角速度则是光滑变化的。

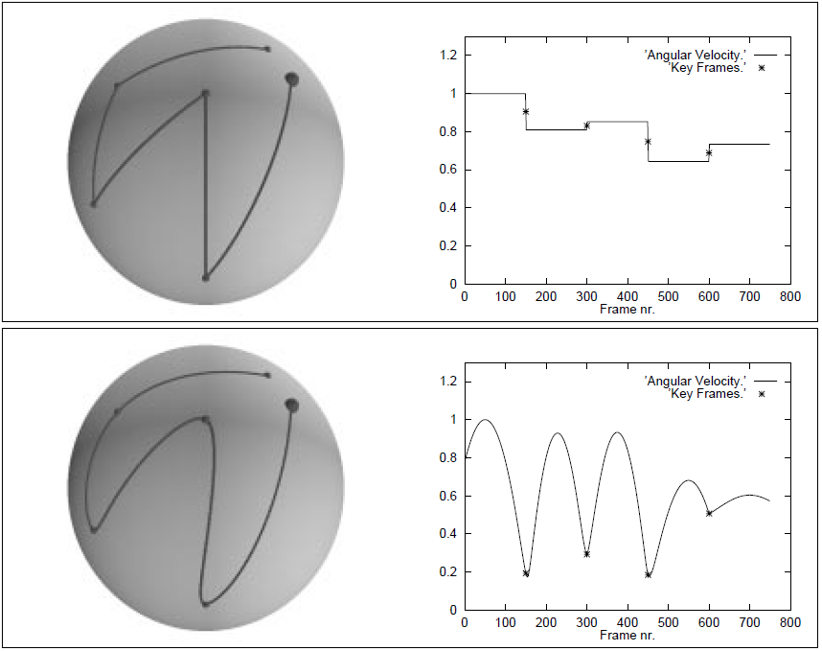
Bézier曲线

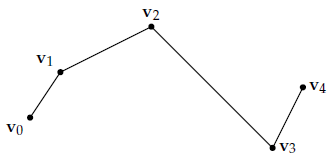
假设我们有一个向量序列，我们可以分别对每一对向量插值。如果我们使用最简单的Lerp插值，就会得到如下图的结果：

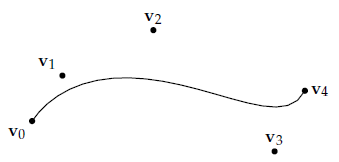
显然这个曲线是连续但不连续，为此，我们可以使用一个四次Bézier曲线，将中间的作为控制点来生成连续曲线。然而这种方法得到的曲线一般不会经过控制点：

关于Bézier曲线的相关知识可以在Wikipedia上找到介绍。

三次Bézier曲线

为了解决这个问题，我们想让生成的曲线（1）经过每个点和（2）一阶导数连续。因此，我们可以分段对每两个向量使用Bézier曲线，其中我们要使用前一个向量和后一个向量生成两个控制点去控制曲线的走势。使用（是端点，是中间的控制点），就能通过一个三次Bézier曲线来插值。

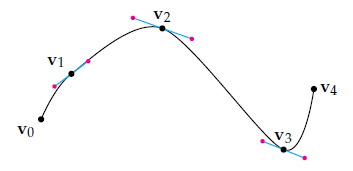
上述做法可以保证曲线经过每个点，但是不能保证曲线在每个点处都是连续的。实际上，对于三次Bézier曲线，只要保证前一个Spline（一对向量生成的曲线）在的控制点与当前Spline在的控制点分别处于最终曲线在处切线对等的两侧：

蓝色的线就是曲线在点处的切线，红色的点就是控制点，每一对控制点分别处于切线对等的两侧。

下面我们来具体了解如何构造一个三次Bézier曲线。

de Casteljau算法

de Casteljau算法可以非常直观简单地构造Bézier曲线，在这里我们只关注三次Bézier曲线的情况。

假设我们有四个向量，de Casteljau算法首先对每一对向量进行线性插值，得到这三个向量：

之后，我们对这两对向量进行线性插值，得到：

最后，我们对进行线性插值得到，这就是我们想要的结果（插值为时）：

整个过程可以总结为下图（）：

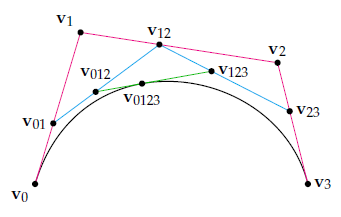
当我们把从变换到时，我们就能得到黑色的曲线。

三次Bézier曲线的过程可以表述为：

é

这里的对于上面的过程来说是线性插值Lerp，对四元数来说则是Slerp。但是由于一个Slerp涉及四个三角函数与除法运算，上式包含了个Slerp，这就会导致极大的效率问题。

Squad

三次Bézier曲线实际上是嵌套了三层一次（one-order）插值，而Squad则使用的是一层二次插值嵌套了一层一次插值。

我们首先是分别对和进行插值，得到和：

之后，我们使用为参数，对进行二次插值，得到最终的：

上述过程可以通过下图阐明（），黑色曲线就是生成的插值曲线：

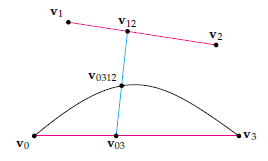
当然，我们也可以把它写成递归形式：

我们成功地将原先的七次Lerp减少到了三次，且生成的曲线与原先的曲线差别也不大，可以看下图的两个对比（左边为Bézier曲线，右边为Squad曲线：

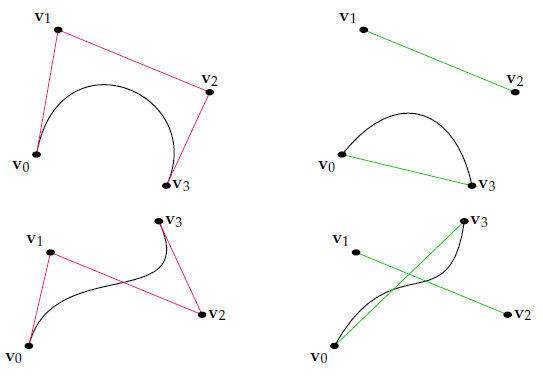
按照Lerp的定义对上式展开，就能得到：

它仍然是一个三次曲线，只不过系数不同。

把它应用到四元数，就能得到我们想要的四元数插值版本：

我们又知道，所以我们又可以把上式写成指数形式：

这个形式对我们后面解出控制点非常有帮助。

Squad应用

现在我们可以使用上式对多个单位四元数进行插值了。假设我们有一个四元数序列，我们希望对每一对四元数都使用Squad进行插值：

接下来就是要找出控制点，为此我们需要前一个四元数和后一个四元数。

找出的基本思路是：让Squad在每个点处都可导，也就是说，我们希望插值时在处的导数，与插值时在处的导数相等：

注意到上面的在对和对插值时都是一样的，与我们之前说的位于切线两端的向量不同，因为它们并非是同一个。在这里，我们假定这样的只有一个，我们只需要通过代数方法求出即可。

通过上面的等式，我们可以求出：

下面是上述结果的推导过程，篇幅较长，不感兴趣的读者粗看即可。所以，和原始版本的三次贝塞尔曲线（包含次Slerp、每次Slerp包含四个三角函数）相比，Squad仅包含次Slerp、每次Slerp包含四个三角函数，二者都需求出两个控制点。总的来说，Squad效率显著高于三次Bézier曲线。

A derivation of control point ：
为方便起见，我们记，我们有：

因为仍然是个单位四元数，所以可以写成：

所以我们就能求出的导数：

从而，我们把代入，有：

我们再把这个结果代回：

同样地，我们可以求出：

我们令两式相等，即得：

最后我们再根据，单位四元数和，得到最开始提出的结果：

你可以验证最后一个等式的正确性。

与两个四元数插值一样，Squad在多个四元数插值时仍然会有双重覆盖的影响，在计算控制点和插值之前，需要先选中一个四元数，检测它与其他三个四元数之间的夹角，如果是钝角就翻转。

Angle、Euler、Matrix、Quaternion之间的相互转换

我们首先总结一下表示旋转的四种方法：

  • Angle Axis（简称为Angle）：任何一个旋转都可以表示为绕一个轴旋转度，这里的旋转轴并不一定是坐标轴。
  • Euler Angles（简称为Euler）：任何一个旋转都可以表示为绕标准坐标系的旋转，旋转顺序可以自定。
  • Matrix Multiplication（简称为Matrix）：任何一个旋转都可以用矩阵乘法表示。
  • Quaternion Rotation（简称为Quaternion)：任何一个旋转都可以用四元数的乘法表示。

这几种表示方法实际上可以相互转化，下面将进行介绍。

Angle转化为其他形式

Angle转化为Euler

我们可以将四元数作为中间媒介进行转换，即先使用Angle转化为Quaternion将Axis Angle转化为四元数：

然后再通过Quaternion转化为Angle将四元数转化为Euler Angles：

其中。

Angle转化为Matrix

在向量绕任意轴旋转的简单推导这篇文章中，我们已经推导出了AngleAxis对应的矩阵形式：

Angle转化为Quaternion

Angle与Quaternion在本质上是一致的，我们在三维旋转定理（四元数型）一节中已经证明过了。所以，对于轴为，旋转角为的Angle表示来说，只需要构造四元数即可。

Euler转化为其他形式

Euler转化为Angle

首先通过Euler转化为Matrix把欧拉角转化为对应的矩阵：

然后再通过Matrix转化为Angle求解对应的（unnormalized）旋转轴与旋转角：

Euler转化为Matrix

在欧拉角、坐标系与旋转顺序一节中我们已经证明了：对于以为顺序的欧拉角旋转，旋转矩阵是：

Euler转化为Quaternion

我们知道，Euler角的旋转是有顺序的，且每一次旋转都是绕标准坐标轴的旋转，所以，我们可以相应地构造出三个四元数去表示这些旋转（旋转顺序为，对应角度为）：

将这三个四元数相乘，即得到结果：

Matrix转化为其他形式

Matrix转化为Angle

给定旋转矩阵，并假设对应的旋转轴是、旋转角度是。显然，如果一个向量平行于，则，从而。

从特征向量的角度来看，是的一个特征向量，它对应的特征值为。从而我们知道：每个旋转矩阵就有一个特征值为。为了求出旋转轴，我们有：

从而我们有：

所以。注意到上面的推导过程在为对称矩阵时不成立，这时候就要按照常规的求特征向量的步骤去求了。

既然我们已经知道了旋转轴，这时只需要找一个垂直于的向量，旋转轴就是和的夹角。

我们也可以从特征值的角度出发。在三维空间内，旋转矩阵的三个特征值分别为，三者之和为，于是：

Matrix转化为Euler

对于旋转矩阵，通过上面Euler到Matrix的转换，我们知道。从而有：

上式仅在，也即时才成立。当时，原矩阵退化为Gimbal Lock，因此无法转化为对应的Euler角。从上面的过程来看，对一个旋转矩阵，至少有两组Euler角与它对应，在某些情况下甚至有无穷解。

Matrix转化为Quaternion

给定矩阵，我们不难通过Quaternion转化为Matrix得到下述关系成立：

所以我们就能解出：

从而得到四元数。

Quaternion转化为其他形式

Quaternion转化为Angle

Quaternion转化为Axis Angle的结果我们已经在三维旋转定理（四元数型）一节中给出。给定单位四元数，我们可以通过变换：

得到它的等价形式，从而，即为旋转角，即为旋转轴。

Quaternion转化为Euler

使用Quaternion转化为Matrix和Matrix转化为Euler的结果，我们能求出以为顺序的欧拉角：

Quaternion转化为Matrix

结果已经由三维旋转定理（矩阵型）一节给出，结果是：

其中。

  1. https://krasjet.github.io/quaternion/quaternion.pdf↩︎

  2. https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles↩︎

  3. http://www.euclideanspace.com/maths/geometry/rotations/conversions/index.htm↩︎

  4. http://number-none.com/product/Hacking%20Quaternions/index.html↩︎

  5. http://number-none.com/product/Understanding%20Slerp,%20Then%20Not%20Using%20It/↩︎

  6. https://web.mit.edu/2.998/www/QuaternionReport1.pdf↩︎

  7. https://www.geometrictools.com/Documentation/RotationRepresentations.pdf↩︎

  8. https://en.wikipedia.org/wiki/Rotation_formalisms_in_three_dimensions#Rotation_matrix_%E2%86%94_Euler_axis/angle↩︎