凹凸贴图(Bump
mapping)是图形学中一种常用的用于改变物体视觉凹凸性的方法,但是网上很多介绍对它的原理和变体都非常模糊,甚至包含一些关键概念的错误。本文将详细介绍凹凸贴图及其变体(Normal
Mapping和Displacement
Mapping)的原理,并在代码上加以实现,以便让读者更好地理解这项技术。
凹凸贴图(Bump Mapping)
现实中有很多物体表面都凹凸不平,比如橘子、砖墙等等,那么我们要如何用图形学的方法去渲染它们呢?最直接的方法就是把这些物体的表面细化为非常微小的三角形,然后走通用渲染流程。但是,由于凹凸分布过于密集,全部按实际模型渲染会导致不可接受的性能开销。
为此,我们能不能假设这种细微凹凸表面是一层贴在光滑物体表面的高度图,每个点都表示了高度的增量。比如我们想得到一个凹凸的橘子,我们可以假想这个橘子本来是一个光滑的球体(尽管橘子不是球体,但这里可以做一个简便的假设),这个球体上的每一点都对应到一个高度图上的一点,记录了当前点的相对高度,比如0.1cm,-0.05cm等等,然后再把这个相对高度应用到球体这一点的实际高度上,就形成该点的凹凸。对所有的点都去计算高度增量,就可以让整个球体变得凹凸不平了。
但是上面的方法还是实际上改变了球体上每个点的位置,而我们计算着色时,实际上只关心这个点的法线,有没有一种方法,可以不去实际改变点的位置,而是计算出改变这个点之后它的法线是怎么变化的,从而从视觉上营造出凹凸感(此时物体本身并没有任何变化)。这就是凹凸贴图做的事情。
纹理空间中的法线
前面已经说到了,我们可以用一张贴图去记录对应点的相对于它法线的高度变化。比如真实空间中的某个点对应纹理坐标为,而,这就说明我们需要把点沿着它的法线方向增高。然而我们并不想实际改变点,而只需要知道改变后的法线就行了。
那么怎么得到呢?首先来看一下在纹理中怎么表示法线。如果我们把纹理的方向视为横轴,方向视为纵轴,再以为竖轴,那么我们就建立起一个以为三轴的纹理空间。每个真实空间中点的法向量都能对应到纹理空间中的向量,但是这个向量的起点在,其中是点的纹理坐标。换句话说,点首先对应了一个纹理坐标,这个纹理坐标上有一个恒定的向量,这个向量和坐标一起,就对应了真实空间中的法向量和本身。
还记得我们上面强调了每个点高度的改变都是沿着它法线方向改变的吗?正是因为这样,我们才要把纹理空间中的每个点处的法向量定义为垂直向上的,这相当于是在纹理空间中模拟真实空间中的法向量,以及沿着法向量改变高度后的法向量如何变化。
这个纹理空间的三轴分别是,每个都定义了一个朝上的法线向量。此外,这个空间还定义了每个点的相对高度。我们关心的是,在这个空间中,点在改变了相对高度之后它新的法线向量是什么。把这个新的法线应用到真实空间中点的法线上,就是改变后的法线。
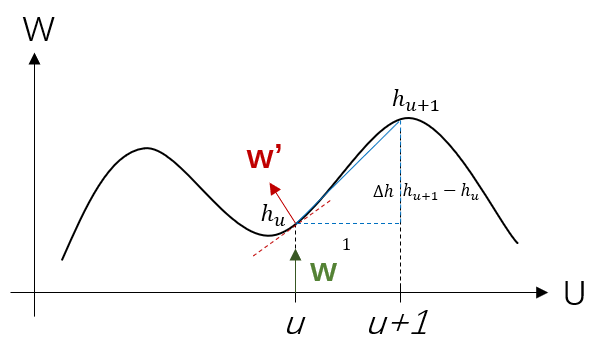
下图表现了这个过程,注意我们先从平面看去。点(先不管)原来的法线是(绿色向量),在应用该点的相对高度之后,新的法线是(红色向量)。
理论上来说,要准确地求出需要知道该点的切线(红色虚线),但这比较困难。我们可以用相邻点去求近似切线,这是很容易办到的。
具体来说,相邻点的高度我们知道是,这样我们就能求出它在方向上的差,值为,而方向上的差值就是,如此一来,我们就得到了一个近似的切线,这里的是一个系数用于调整斜率。知道了切线,我们就知道了法向量为。
对于真正的三维纹理空间也是一样的,对于平面,方向的差值为,对于平面,方向的插值为。这样一来,近似法线就是。这就是纹理空间中变换相对高度后的法线。
纹理空间,世界空间与TBN矩阵
下面的问题是,既然我已经知道了纹理空间中变换高度后的法线,同时也知道了世界空间中原本的法线和纹理空间中原本的法线,怎么才能得到世界空间中变换高度后的法线。
现在我们再捋一下世界空间和纹理空间这两个空间。在世界空间中,所有的向量都是一个绝对值。比如现在三角形上的一个顶点,它当前的法线是,如果此时把三角形连同点任意旋转,那么的法向量也会随之改变,比如到了。然而,在纹理空间中点对应的纹理坐标和其之上的法向量是没有改变的!同时,使用上述过程计算出来的纹理空间中新的法向量也是没有改变的!这也就意味着纹理空间中的向量是一个相对值。无论世界空间中的点如何运动,纹理空间中变化前和变化后的法向量都不会随之运动,纹理空间中的法向量和世界空间中法向量始终保持了一致的相对位置关系!
所以,我们现在的目标,就是要求出一个变换,对每个特定的点,它能将世界空间中的法向量变换为纹理空间中的一个法向量;那么它的逆变换,就能把纹理空间中的法向量映射为世界空间中的法向量。我们想要的,就是。
我们不妨先考虑逆变换,它可以用一个矩阵表示。我们实际上很容易知道,这是因为纹理空间中改变前的法向量需要和世界空间中改变前的法向量相对应:。我们还需要另外两个方程才能解出。为此,我们可以通过点所在的三角形求解。
为此,假设三角形的边向量为,边向量为;在纹理空间中,对应的向量为,对应的向量为。其中,。那么根据我们的定义,显然有下述方程成立:
其中。
整理成矩阵相乘,就有:
上式需要保证逆矩阵存在,即。
但现在得到的两两之间并不保证互相垂直,这是因为从上面的式子我们不难发现和是关于的线性组合,所以这两个基仍然在三角形所在的平面上,而这个平面不一定和向量正交,而且和本身也不一定正交。
所以作为求解的最后一步,我们还要把这三个基正交化,我们可以使用Schmidt正交化:
这样一来,就是两两正交的单位向量了,从而就得到了逆变换。由上面的过程可知,我们其实不用真正解出,因为它可以通过与的叉乘求得。
你也许会问,上面的推导过程我们为什么不直接用三角形的三个顶点,而要去用它的边呢?这是因为,向量和点本质上是不同的,尽管它们都可以用一个三维坐标表示。比如三维空间中的一个物体,它某个点的法向量是,把物体整体平移了之后,这个点的坐标发生了变化,但是它的法向量还是。既然我们只是向量感兴趣,那么所有的操作都是基于向量进行的。这一点务必理解。
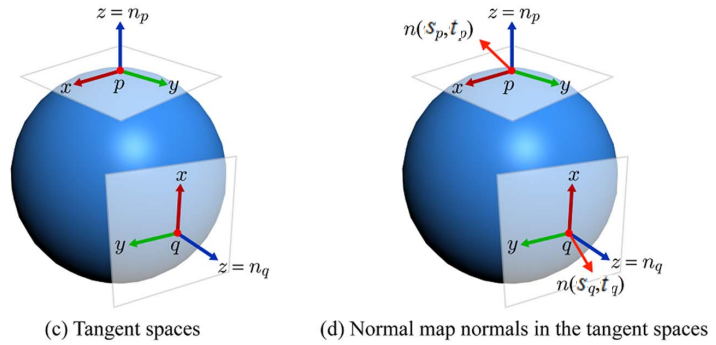
现在,定义的空间就是以为基的空间,这个空间的“轴”就是,正好与世界空间中点的原始法向量重合,而则定义了的切平面。对纹理空间中任意的法向量,都可以左乘这个矩阵得到对应的世界空间中的法向量。它定义的空间就称为切线空间,而矩阵就是所谓的TBN矩阵。
如果你还不理解,就这么思考。现在在纹理空间中有一个法向量,它的坐标是基于这三个标准正交基表示的。现在,需要把这个标准正交基“旋转”到世界空间中,让和原来的法向量对齐,再让另外两个轴旋转到某一个方向,这个方向能够反应三角形两条边的纹理变化方向。这样一来,就能表示在这个新的基上的线性组合,得到的就是真实世界中变换后的法向量。这个过程如下图所示(就是这里的,就是这里的,定义的空间就是切线空间,它位于真实空间内):
如果你认真思考,就会问出下面两个问题:
- 为什么需要正交化?不是我们直接出了了吗?为什么不能直接用它作为呢?
- 正交化之后的基和原始纹理空间的关系是如何的?能保证映射到真实空间中的法向量和原始法向量的相对位置关系正确吗?
下面我们来依次回答这两个问题。
为什么要正交化
这个问题的答案很简单:因为计算改变后的法向量时是基于纹理空间进行的,而纹理空间一般来说(暂不考虑畸变的情况)就是由三个标准的正交基组成的。
举个例子,某点的法向量是,是个可以任意改变的向量,它在纹理空间中对应了点的一个向量,这个我们之前已经明确了。现在,假设我们计算出来的改变后的法向量正好在UV平面上,也就是与垂直,那么此时,如果我们直接用把映射回真实空间,我们会得到一个在三角形所定义的平面上的一个法向量,这个法向量不一定和原来的法向量垂直,因为三角形不一定和垂直。显然,与就没能保持在纹理空间中与一致的相对关系,即垂直关系。
所以,为了得到正确的相对关系,我们必须让求得的保持正交关系,正如在纹理空间中一样,这样才能让纹理空间中变换前后的法向量与真实空间中变换前后的法向量保持一致的相对关系。
那这样一来,不就不能映射回了吗?对的,但是我们实际上真正关心的是法向量而不是三角形的某个边,它只是用来帮助我们构造TBN矩阵的工具,所以映射不回去也没有关系了。
法向量的方向
紧接着就会有另一个问题:正交基,也就是切线空间有了,但是你怎么保证向量的方向是正确的呢?或者说,经过变换后的真实空间的法向量的反向是否是正确的。你可以想象变换后的法向量在绕着原来的法向量以相同的夹角旋转(它们的起点相同),从而可以形成一个锥形,那么到底哪个方向才是真正的呢?
答案是:在凹凸贴图中不能保证方向的正确性,但误差是可以接受的。回想一下,我们在求解时,让纹理空间中的对应到真实空间的法向量,这是没有问题的。然后把三角形的边和它在纹理空间中的纹理坐标向量进行对齐,进而求得。这里其实做了一个假设,三角形内部的点的纹理坐标是可以通过三角形三个顶点的纹理坐标进行线性插值得到的。当然严格来讲,这不一定成立,因为任何一个点的纹理坐标都是可以任意指定的,但是一般来说,我们在制作纹理贴图的时候,会把模型作为一个整体制作,这基本上也就是一个线性关系。
因为我们是把映射到、把映射到的,只要纹理贴图制作得比较规范,即便正交化了,经过TBN矩阵转换后的世界空间的法向量也不会偏离真实的法向量太远。这里可以顺便回答为什么在进行正交化的时候是而不是,这是因为在纹理空间中,对应了,对应了,如果要得到,就只能是。这对应到真实空间中,就是。
值得一提的是,在法线贴图中是可以保证变换后的法线的方向是正确的,这个我们下面讲到法线贴图的时候稍加解释。
上面说了这么多,切线空间带来的最大好处是,它和真实空间是一种相对关系,这意味着我们不需要为模型在每个不同的位置都制作贴图,极大减少了工作的复杂度,也更加灵活。
法线贴图(Normal Mapping)
在了解了凹凸贴图之后,法线贴图就很自然了。在凹凸贴图中,纹理空间中变换后的法线是要手动去计算的,那为什么我们不直接把法线存储在这个点呢,就像一张RGB纹理图一样。
在RGB纹理图中,每个点的RGB值都在中,但是法线的每个元素都在中。所以要用RGB的贴图存储法线,就要对法线先加一,再除以二,就能把值的范围规约到中。那么为什么我们看到一般的法线贴图都偏蓝色呢?这是因为法线的值比较大,就对应到RGB的蓝色值偏大,所以使得整个图呈现偏蓝的颜色。
下图左侧是凹凸贴图,用灰度值表示每个点的高度;右侧是法线贴图,每个点都是一个RGB值。

在从法线贴图中获取了变换后的法线之后,仍然需要像凹凸贴图一样,首先计算得到,然后再正交化得到TBN矩阵,最后左乘TBN矩阵就了得到世界空间中变换后的法线。
现在可以回答之前的一个问题:为什么使用法线贴图得到的变换后的法向量就能保证它和的相对关系是正确的?这是因为,是一个正交矩阵,它代表的是把纹理空间中的法向量转换到世界空间中的法向量;那么它的逆(也就是它的转置,因为是正交矩阵),就能够把世界空间中的法向量变换到纹理空间中的法向量。所以,给定一个模型(或者三角形),在制作它对应的法线贴图的时候,只要按照的方式在纹理空间中存储法线(是艺术家制作决定的),就能通过逆变换还原真实空间的法线。也就是说,只要存储和调用都用这样的同一套变换矩阵,得到的法线就一定是正确的。
光线、观察方向等实际上也都是一种法向量,它自然也能被映射到纹理空间中,直接和进行计算,而不需要把所有点都经过TBN矩阵变换到世界空间中再做Shading,这样一来就降低了计算量。
GAMES 101 作业三中的Bump
Mapping
GAMES101的作业三也让我们实现了一个简单的Bump
Mapping,下面是代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
Vector3f n = normal.normalized();
float d = sqrt(n.x() * n.x() + n.z() * n.z());
Vector3f t (-n.x() * n.y() / d, d, -n.z() * n.y() / d);
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN.col(0) = t, TBN.col(1) = b, TBN.col(2) = n;
float u = payload.tex_coords.x(), v = payload.tex_coords.y();
float w = payload.texture->width, h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColorBilinear(u + 1.0f / w, v).norm() - payload.texture->getColorBilinear(u, v).norm());
float dV = kh * kn * (payload.texture->getColorBilinear(u, v + 1.0f / h).norm() - payload.texture->getColorBilinear(u, v).norm());
Vector3f ln (-dU, -dV, 1);
normal = TBN * ln;
Eigen::Vector3f result_color = normal.normalized();
return result_color * 255.f;
}
|
首先定义了环境光、漫反射和镜面反射的系数,然后定义了光线和观察位置,之后求出了TBN矩阵与纹理空间中的法向量,最后转换到了世界空间中进行着色。
这里通过dU和dV得到的就是我们一开始讲的纹理空间中变换后的法向量,只不过这里是在乘了TBN矩阵之后再进行的归一化。
但是这里的TBN计算方式,和我们上面提到的完全不一样。倒是正确的,它直接用了当前的法向量:
1
| Vector3f n = normal.normalized();
|
但是计算就完全让人摸不着头脑了(可以通过叉乘实现):
1
2
| float d = sqrt(n.x() * n.x() + n.z() * n.z());
Vector3f t (-n.x() * n.y() / d, d, -n.z() * n.y() / d);
|
翻译成数学公式就是:
可以验证这是一个与垂直的单位向量。
这两行代码是什么意思呢?其实,这里这里是对向量进行了旋转操作。如下图所示,先把拆成它在XZ平面和Y轴上的分量和。现在我们的目标就是在由和所定义的平面上的任意一个向量,都得到它在同一个平面上的垂直向量。对来说,这个向量就是;对来说,这个向量就是。所以本质上我们是要求一个旋转矩阵,它可以得到该平面上与一个向量垂直的向量。
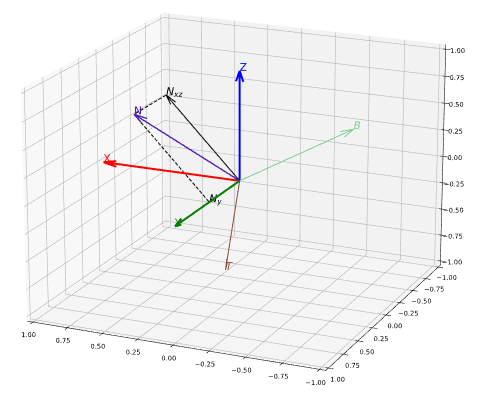
这个变换很简单,就是先将它绕着Y轴旋转°,这里的是与X轴形成的夹角,得到的向量会在平面XY上;然后绕着Z轴旋转90°;最后绕Y轴旋转°,得到的向量就是与给定向量在平面内垂直的向量。这三个连续操作可以写成三个矩阵的乘积:
再由,可知,变换矩阵为:
所以,变换后的结果就是。
所以,从根本上讲,切线空间除了需要被作为Z轴是明确的之外,剩下的两个轴(实际上是一个轴,也就是所谓的Tangents,另一个轴可以通过叉积求得)都是可以手动定义的。只要在制作存储法线贴图和使用法线贴图时保持一致即可。
位移贴图(Displacement
Mapping)
分析Bump mapping和Normal
mapping不难发现,它们实际上是通过改变法线制造一种假象,这时候物体本身没有丝毫变化。这种方法难以处理由凹凸表面带来的自阴影,并且物体的边界会露馅。
Displacement
mapping真的去改变每个点在空间的位置,从而得到更加真实的结果。
下面是GAMES101 作业三中关于displacement mapping的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
| Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
Vector3f n = normal.normalized();
float d = sqrt(n.x() * n.x() + n.z() * n.z());
Vector3f t (n.x() * n.y() / d, d, n.z() * n.y() / d);
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN.col(0) = t, TBN.col(1) = b, TBN.col(2) = n;
float u = payload.tex_coords.x(), v = payload.tex_coords.y();
float w = payload.texture->width, h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColorBilinear(u + 1.0f / w, v).norm() - payload.texture->getColorBilinear(u, v).norm());
float dV = kh * kn * (payload.texture->getColorBilinear(u, v + 1.0f / h).norm() - payload.texture->getColorBilinear(u, v).norm());
Vector3f ln (-dU, -dV, 1);
point += (kn * normal * payload.texture->getColorBilinear(u, v).norm());
normal = (TBN * ln).normalized();
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
float square_distance = (light.position - point).squaredNorm();
Vector3f l = (light.position - point).normalized();
Vector3f v = (eye_pos - point).normalized();
Vector3f n = normal.normalized();
Vector3f h = (l + v).normalized();
Vector3f I = light.intensity;
Vector3f ambient_light = ka.cwiseProduct(amb_light_intensity);
Vector3f diffuse_light = kd.cwiseProduct(I / square_distance) * std::max(0.0f, n.dot(l));
Vector3f specular_light = ks.cwiseProduct(I / square_distance) * std::pow(std::max(0.0f, n.dot(h)), p);
result_color += ambient_light + diffuse_light + specular_light;
}
return result_color * 255.f;
}
|
仔细观察代码,不难发现它最核心的代码就一行:
1
| point += (kn * normal * payload.texture->getColorBilinear(u, v).norm());
|
这一行代码的意思是点在空间中的位置实际地被改变了。这会影响下面光照距离、观察方向、光照方向的计算,从而改变着色结果。
参考文献
圖形學系列
Games101-Homework3-NormalMaps and BumpMaps and
DisplacementMaps
切线空间(Tangent
Space)完全解析
LearnOpenGL
CN法线贴图
深入浅出之切空间



