Remedies for Cinemachine's Lock-on Camera

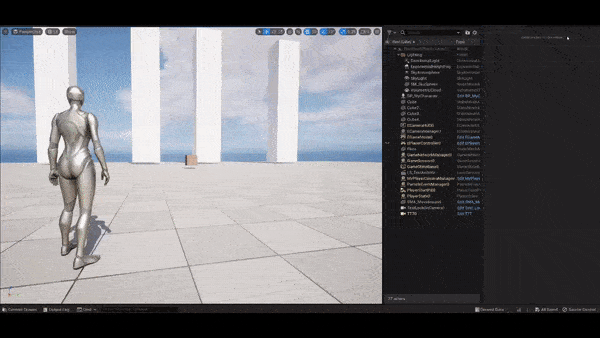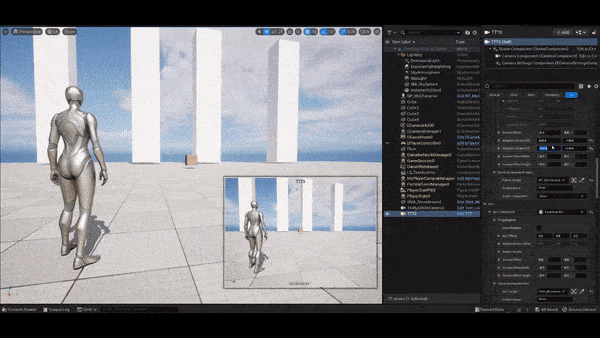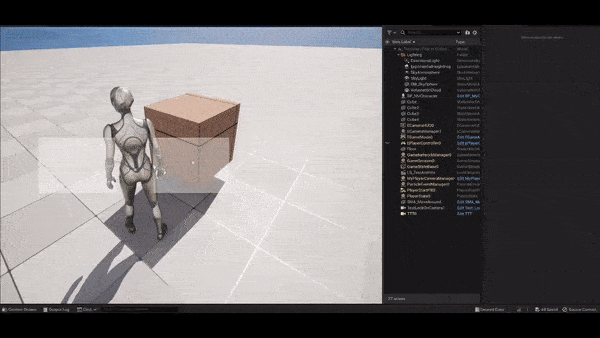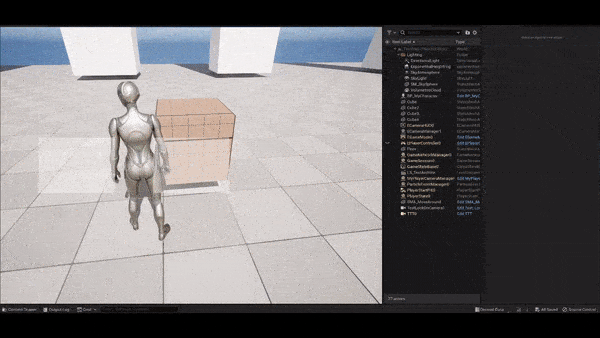
Lock-on cameras in Cinemachine typically mean cameras with components Framing Transposer and Composer. Cameras with these two components follow the protagonist while looking at another object, just like when you are fighting with a BOSS. However, in certain situations the camera will keep rotating around the protagonist and the look-at object, creating a very unnatural artifact for the player. This blog post explores how this phenomenon happens and how to remedy it.

What happens to lock-on cameras in Cinemachine

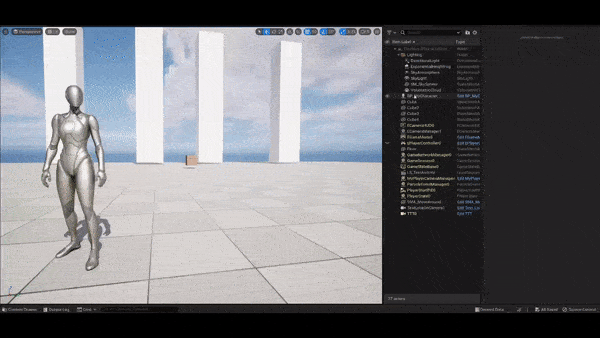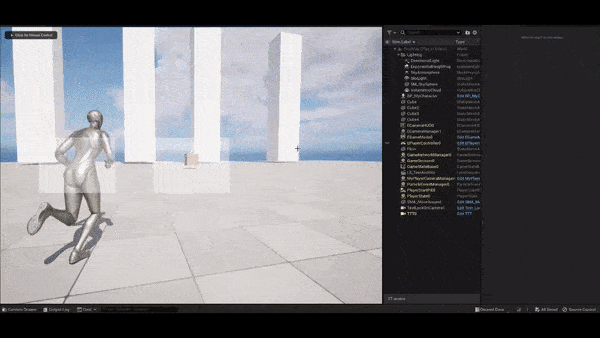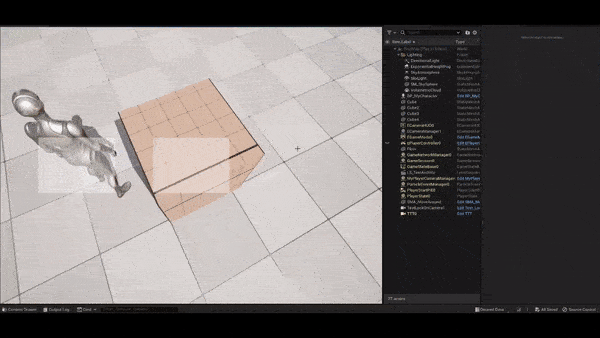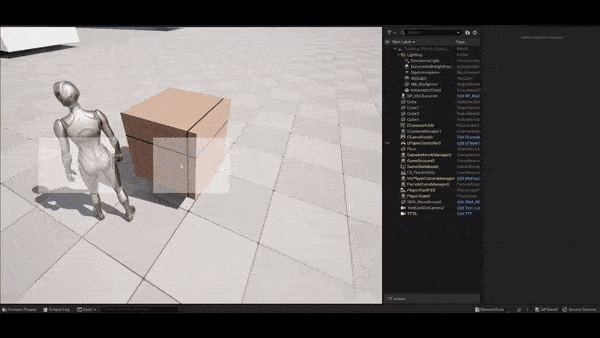
Lock-on cameras (the combination of the Framing Transposer and Composer components) in Cinemachine suffer from severe infinite rotation around the follow target and look-at target under particular camera settings and when the two targets are close to each other. We will first briefly explain why this happens.

Considering a sphere centered at the follow target position , the camera lies on the surface of the sphere. We further assume the camera distance to is , that is the radius of the sphere, the picth is and yaw . Then the camera position is where and is

is camera's relative position on the sphere with regard to , and is camera's positional offset that is projected into screen space to ensure displays at the correct position on screen. is a user-specified parameter, in range indicating the normalized screen position of , and is camera's field of view, usually .

Derivation of is omitted. For interested readers, please refer to this blog post.

Assuming the look-at position is , we have the following equation hold:

where is a positive value. Rearrange this equation, we have:

which reduces to

This gives us three equations. By substitutions, we have:

However, the problem here is the left hand side can ba smaller than or greater than when the denominator -- the projected distance between the follow target and the look-at target -- is small. We cannot simply clip it as it will raise incorrect yaw and pitch results.

Remedy #1: restricting the Screen X/Y parameter

The first remedy is quite intuitive: we concurrently shrink , i.e., the value of as the denominator gets small. We can use the following simple equation to modify according to current value of :

where and are user specified parameters respectively indicating the distance from which starts to shrink and reaches zero (when ).

This technique is simple and effective in reducing the chance of infinite rotation by cameras, but creates a weird effect that the follow target will gradually arrive at the center of screen. You can tweak and so as to maintain a trade-off.

Remedy #2: pushing away the look-at object

Analysis

Now that this problem is caused by camera's sensitivity to the projected distance , we can create a fake aim target whose position is different from the authentic one while keeping a relatively large and maintaining camera's orientation. Two goals:

• The distance between the follow target and the fake aim target has a minimum value, denoted by radius .
• The camera now looks at the fake aim target and maintains the same orientation as the real aim target.

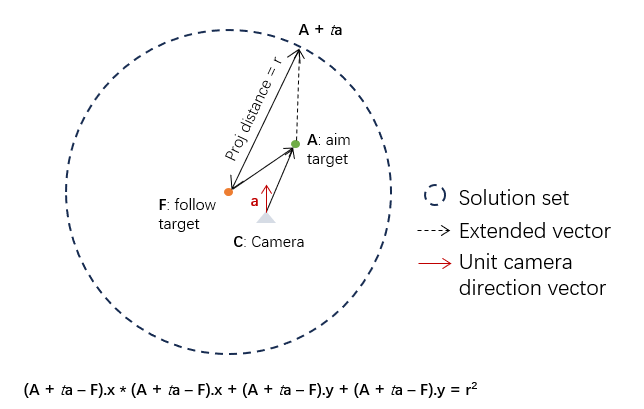
The second condition implies that the aim target should be extended along the direction from the camera to the aim target. Based on the the above equations, it is the direction of the camera forward, i.e., . The magnitude of the additional vector is denoted by such that the distance between (the follow target) and (the stretched aim target) is .

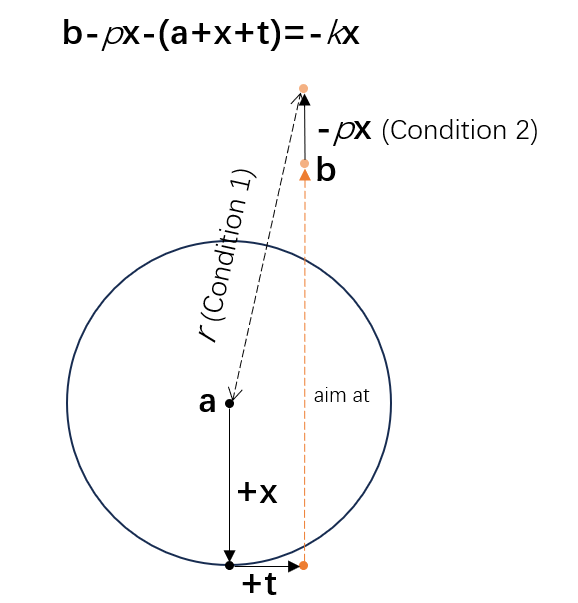
But both conditions cannot be satisfied simultaneously. Let's assume term has an invalid value going beyond . For the sake of brevity, we assume and and the target radius is .

With the the stretched aim target , we can rewrite the starting equation as:

Rearranging this equation gives us:

The only difference is the coefficient, i.e., from to . Using the same substitution, we still reach the result of . The equation still has no real-valued solution.

We must relax one of the two conditions. As we would like to keep a minimum projected distance between the follow target and the aim target, we can relax the second condition, allowing the aim target to show at a different screen position by dynamically adding an offset to the aim target. Then, the real aimed position is the point being offset from the original aim target.

Method

So what is the offset , which is added to the aim target to form the real aim position ? The intuition is to maintain a relatively static positional relationship between the follow target and the aim target when their projected distance is less than . The relationship is determined by the pitch angle in the frame where the projected distance just goes inside .

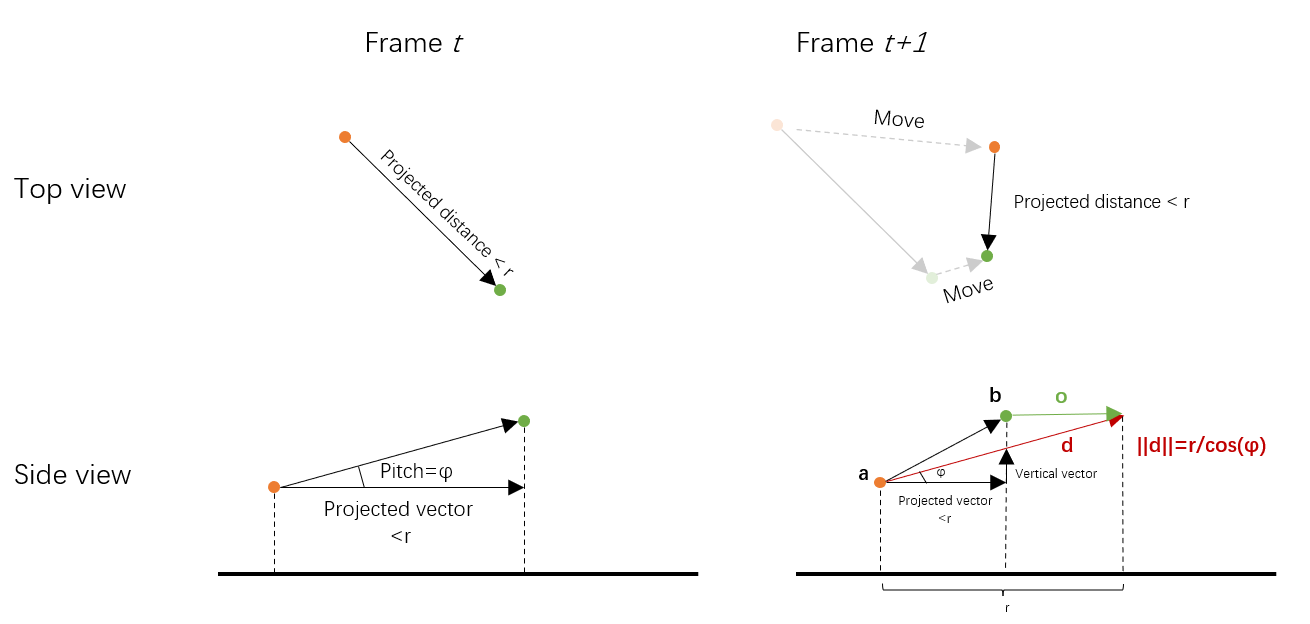
The above figure shows how to keep the so-called static relationship. In frame , the projected distance for the first time is less than . At this time, we compute and cache the pitch angle formed by the follow-to-aim directional vector and the XY plane. The pitch angle is denoted by . In next frame, i.e., frame when both the follow target and the aim target move but still have a projected distance less than , we try to restore the real aim target position which satisfies two conditions: (1) its projected distance to the follow target is exactly , and (2) the pitch angle maintains as . Through a series of simple vector calculations, we obtain , the directional vector from the follow target to the real aim target position. The offset vector is then readily available.

Question: why do we maintain a static pitch angle? This is of course not definite, but a static pitch angle circumvents the problem of camera jitters caused by drastic pitch change.

The following pseudo code shows the process (called in each frame):

Vector3 FollowPosition = GetFollowTarget().Position;
Vector3 AimPosition = GetAimTarget().Position;
float ProjectedDis = VectorProjectDistance(FollowPosition, AimPosition);

if (ProjectedDis < Radius)
{
  if (!bInProcess)
  {
    bInProcess = true;
    CachedPitch = FindLookAtRotation(FollowPosition, AimPosition).Pitch;
  }

  Vector3 FollowToAim = AimPosition - FollowPosition;
  Vector3 Projected = ProjectToXY(FollowToAim);
  Vector3 Vertical = Vector3(0, 0, 1) * Projected.Length() * Tan(CachedPitch);
  Vector3 Direction = Projected + Vertical;

  Direction.Normalize();
  Direction *= Radius / Cos(CachedPitch);

  Vector3 Offset = Direction - FollowToAim;
}

The code snippet is quite simple and neat. It follows several steps:

• If in current frame the follow target steps into the range of radius , then cache the pitch .
• For each frame where the original projected distance is less than :
  • Project the original directional vector FollowToAim.
  • Get the vertical vector Vertical using .
  • Get the calibrated directional vector by adding the projected vector and the vertical vector.
  • Normalize the directional vector.
  • Multiply it by the length . This gives us .
  • The offset vector .

The following figure shows how this method does to remedy the problem. As the follow target enters the range of radius, the aim target begins to be offset. Seems good so far.

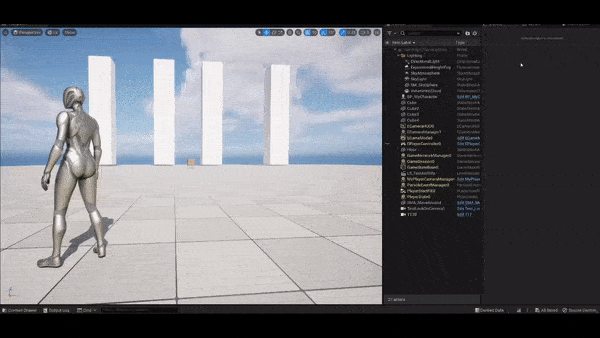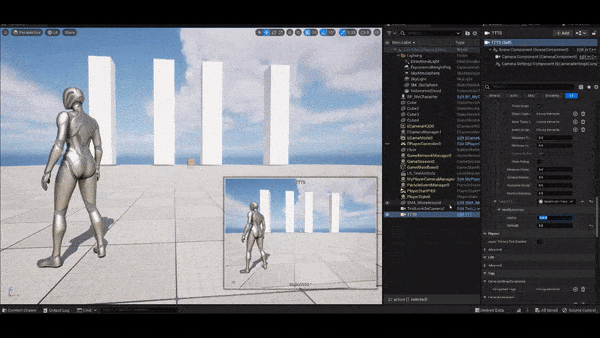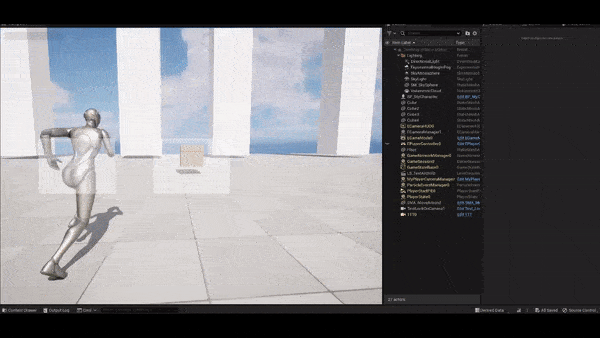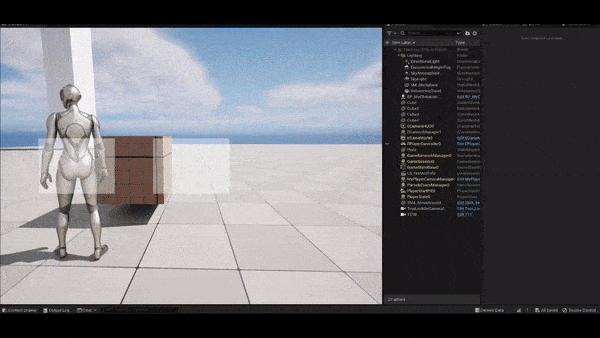
Improvement: blending with another aim target offset

If we only consider the first condition, i.e., the projected distance is equal to a fixed value , it's easy to see that all feasible aim positions lie in the surface of a cylinder with center and radius . The solution set is denoted by . The vanilla method gives only one possible point . In fact, we can choose another feasible point and blend them to create a more natural camera feeling.

Recall that at the beginning of this section, we analyzed that extending the aim position along the direction of camera-to-aim will not change the aim target's position on screen. This is a nice property because what we exactly want to preserve is the screen space position.

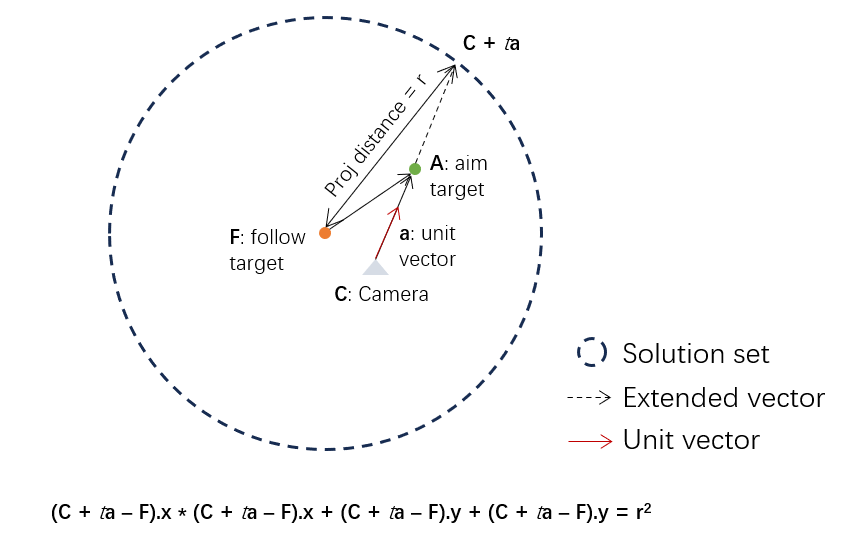
We use the above figure to illustrate how to compute this offset. Let be the follow target, the camera, the aim target, and a unit vector along the direction from to . Assume the point is the target point to which the projected distance from is . This can be formulated as:

is the vector from to , and we use to represent it. This equation can be expanded as:

This is a quadratic function so we can readily solve it. But be careful when this equation is unsolvable.

Pseudo code to compute this offset is shown as follows:

Vector3 FollowToCam = GetCamera().Position - GetFollowTarget().Position;
Vector3 CamToAim = GetAimTarget().Position - GetCamera().Position;

float CurrentLength = CamToAim.Length();
float TargetLength = CurrentLength();
CamToAim.Normalize();

// At^2 + Bt + C = 0
float A = CamToAim.X * CamToAim.X + CamToAim.Y * CamToAim.Y;
float B = 2.0 * (FollowToCam.X * CamToAim.X + FollowToCam.Y * CamToAim.Y);
float C = FollowToCam.X * FollowToCam.X + FollowToCam.Y * FollowToCam.Y - Radius * Radius

float Delta = B * B - 4.0 * A * C;

if (Delta > 0)
{
  TargetLength = (-B + FMath::Sqrt(Delta)) / (2.0 * A);
}

float Magnitude = TargetLength - CurrentLength;
Vector3 Offset_2 = CamToAim * Magnitude;

// blend the two offsets
Vector3 FinalOffset = (1 - Strength) * Offset + Strength * Offset_2

Note that using the above calculation, the linearly blended vector may not maintain a length of . But the error is acceptable. If you want to have the perfectly accurate result, you can resort to the spherical interpolation.

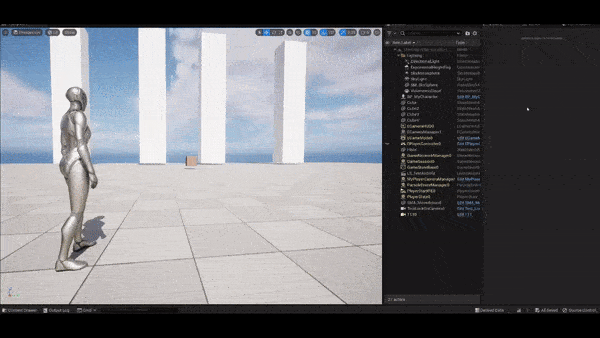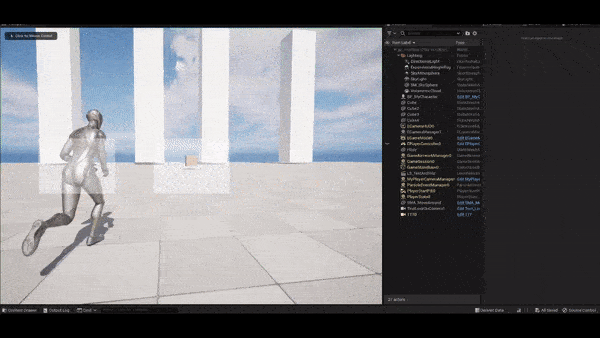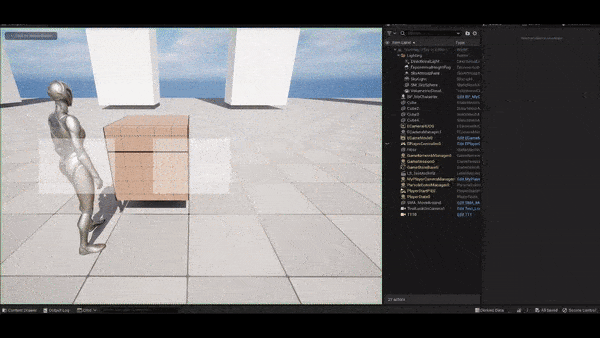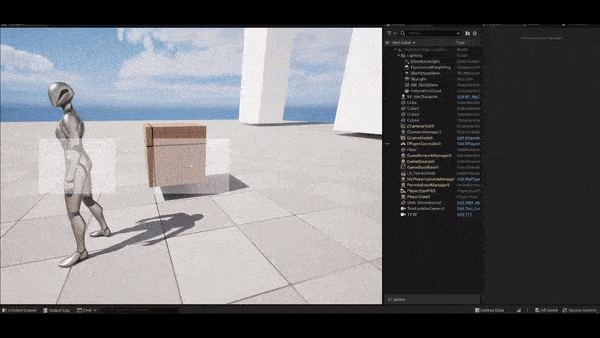
As shown in the figure, we can see the blended offset combines well both worlds: to keep a fixed screen position and to avoid infinite rotation when the projected distance is small. The parameter strength should be chosen differently under different situations. Generally, a value between 0.5~0.8 performs well.

Camera's forward as offset direction

We can also apply another type of offset to bias the aim target position on screen, that is, the camera's forward direction projected onto the XY plane, shown in the following figure.

Different from the previous case, this time we offset the aim target along the direction of camera's forward vector (projected onto the XY plane), denoted by . The expected point is which satisfies:

We can use the same technique to solve this equation. Pseudo code is given as follows:

FVector CamDir = UKismetMathLibrary::ProjectVectorOnToPlane(GetOwningActor()->GetActorForwardVector(), FVector(0, 0, 1));
CamDir.Normalize();

A = CamDir.X * CamDir.X + CamDir.Y * CamDir.Y;
B = 2.0 * (FollowToAim.X * CamDir.X + FollowToAim.Y * CamDir.Y);
C = FollowToAim.X * FollowToAim.X + FollowToAim.Y * FollowToAim.Y - Radius * Radius;
Delta = B * B - 4.0 * A * C;

if (Delta > 0)
{
  Magnitude = (-B + FMath::Sqrt(Delta)) / (2.0 * A);
}

CamForwardAddition = CamDir * Magnitude;

Intuitively, this offset encourages the aim target to maintain its screen space position while constraining the camera's pitch because the real aim position is now horizontally farther and the camera does not need to raise its head to orient to it. This is a trade-off between screen space position and camera's pitch angle, and can be combined with the other two methods.

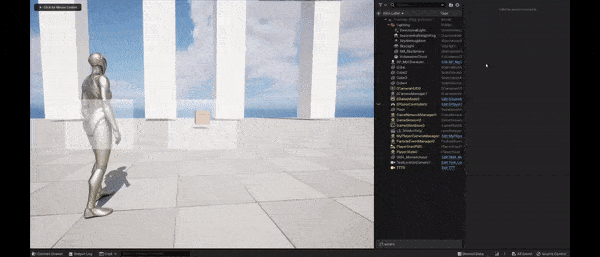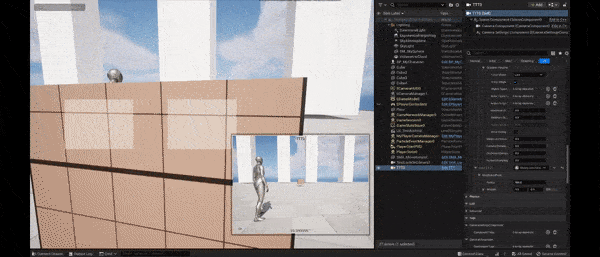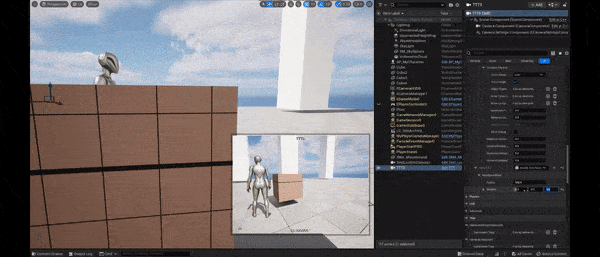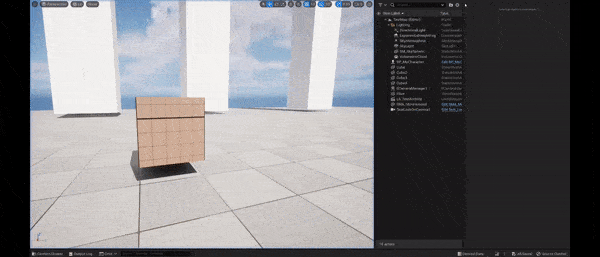
Using only this offset, we see that the aim target preserves well its screen space position. But the cost is an increased time delay for the camera to lock on the aim target. Interpolating it with the first offset, this artifact disappears.

Summary

In this post, three methods to remedy the infinite rotation issue are proposed, where each has its merits and defects.

• Pitch Offset: This offset is applied to the aim target so that the real aim position and the follow target forms a fixed pitch angle. It will never cause infinite rotation but the aim target will be biased on screen space.
• Camera-to-Aim Offset: This offset is applied in the direction from camera to the aim target and still cause infinite rotation. It is used to pull back the other two offsets so that the aim target manages to maintain at the correct screen space position.
• Camera Forward Offset: This offset is applied along the projected camera's forward direction. As this offset is parallel to the XZ plane, it will not cause the infinite rotation problem is appropriately set. It will not change the aim target's screen position but may increase the delay when the camera looks at the aim target.

In practice, it's recommended to interpolate these three methods to achieve a more natural and smooth result.