Inertialized Camera Transition

Typical methods to transition from one camera to another camera is to leverage pre-defined blend curves and a specified blend time to control the speed and smoothness of blending. However, one problem with curves is that they don't provide velocity continuity at the start and end of transition, which usually results in a visual artifact either a sudden stop or a sudden launch. Fortunately, inertialization provides such continuity. In this blog post, I will attemp to introduce inertialization into camera transition, uncovering its potential for a very smooth and nice camera transition process.

Inertialization in Animation

Inertialization is an important technique used in animation to eliminate tne evaluation cost for the source animation and maintain a smooth transition feeling.

What inertialization does is to employ a fifth-order polynimial to interpolate the difference between the source value and the target value .

The update expression at each timestamp is:

where is the transition time, is the output value at and is the target value at .

To ensure the continuity at transition start and transition end, must meet:

For (1), we have:

For (2)~(6), we can derive:

where and are respectively the velocity and acceleration of the source when transition starts. Then we can use the update formula to obtain the output value at timestamp .

For vector type, inertialization is not directly applied to each of the vector components independently. Rather, it's applied to the magnitude of the vector and keep the direction fixed.

More concretely, given a source vector and target vector when transition starts, the difference vector is decomposed into the direction and the magnitude . The difference vector for the previous frame is and its magnitude is the projected length onto the current direction: . The velocity is thus . By this, the inertial polynomial is constructed and the output vector for each timestamp is:

For rotation type, inertialization is applied to the angle of the axis-angle decomposition of rotations. The difference rotation for current frame is where is the source rotation (quaternion) and is the target rotation. Then, it's decomposed into the axis and angle: , . The previous rotation is , and its rotation angle projected onto the current rotation axis is . Then the velocity is and the update rule is:

What Do We Want for Camera?

If we see camera as a special type of joint, we can seamlessly apply inertialization to the camera transition. Before we introduce how we actually implement inertialized camera transition, we must keep in mind what we really want for camera transition.

• Maintain velocity and (possibly) acceleration continuity when transiton starts and ends. Different from animation, camera serves as the eye through which the players see the game world, and thus it is very sensitive to discontinuous positional and rotational jitters. In many cases such as transitioning from gameplay camera to cinematic camera or the other way around, a continuous transition significantly improves the sense of immersiveness without interrupting game feelings.
• Control over the blend time for most of the time, but also need a way to automatically choose blend time in case we want to constrain the acceleration. During transition, we don't want the movement to change too fast, that is, we'd like to restrict the acceleration. By doing so, the blend time can automatically selected given a viable maximum value of acceleration.
• Control over the shape of blend curve. It's about the speed of movement at each timestamp. Do we want to keep a linear curve on the entire transition process? Or do we want to keep it slow as the transition start and end, and as fast as possible in the middle of transition?

So, does inertialization meet these requirements? Well, not exactly. Inertialization meets the first requirement but not for the second and the third. We must modify the vanilla inertialization algorithm to adapt it to our needs.

Modified Inertialization

Control Over The Blend Curve

Let's start with controlling the shape of the blend curve. From what we derived above, the inertialization polynomial is fixed given the initial values. We can interpolate with an additive function weighted by a weight function to control the overall shape of the final blend curve:

The new output value is updated using :

As before, we expect to have the same properties as do, i.e.,

To meet these requirements, we can find such that satisfies these conditions and relax only to be continuous on . For example, can be a simple linear function, or an easing function or a cubic curve.

There are many options for . We choose a simple logarithmic form of :

where controls the shape of the weighting function and is the maximum value can reach on . The larger is, the faster will get to its max.

On , we flip and translate so that and are symmetric to . By definition, .

Overall, the weighting function is:

The following figure shows the the weighting function and the interpolated curve given and the linear additive function with different and :

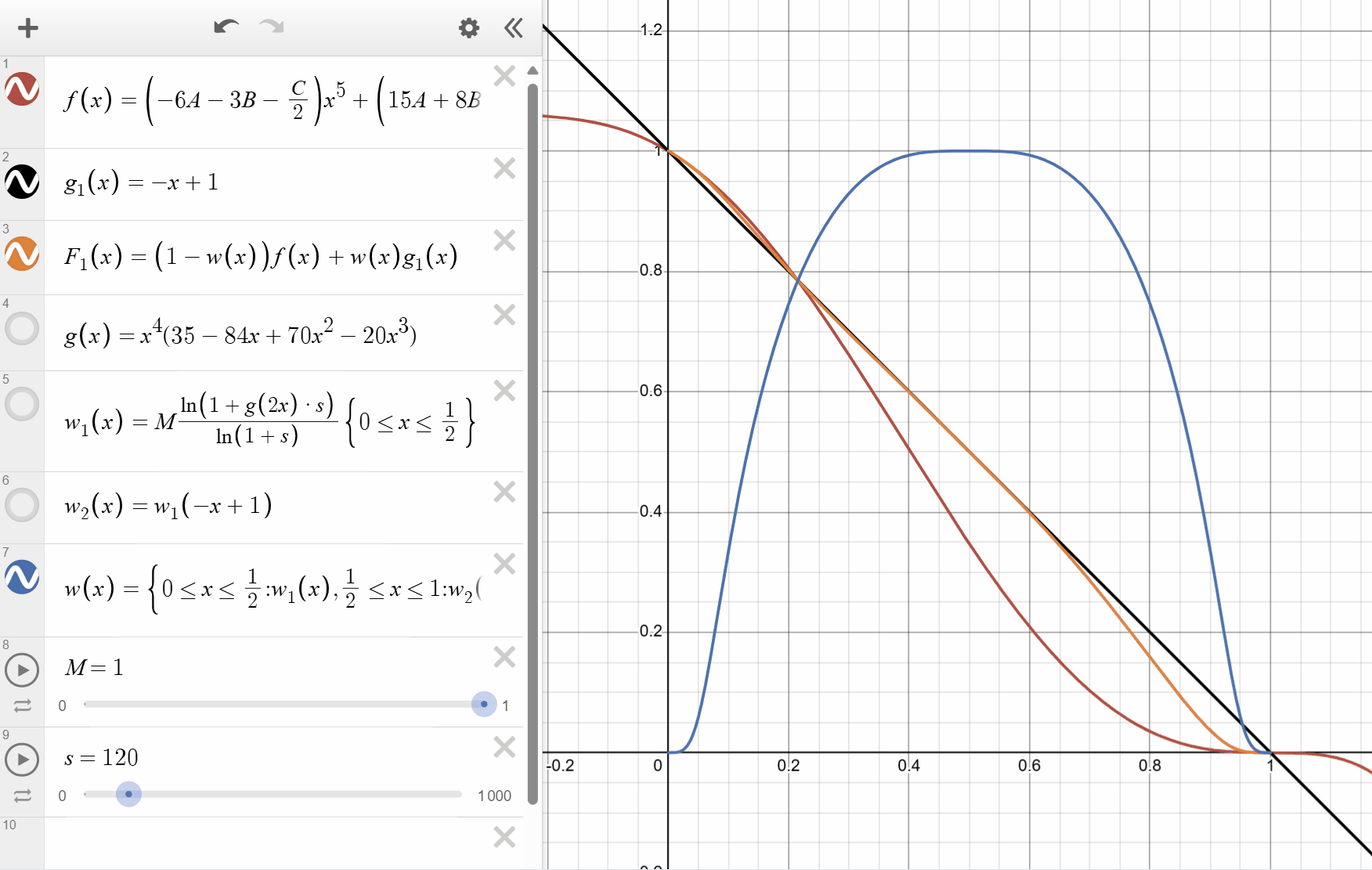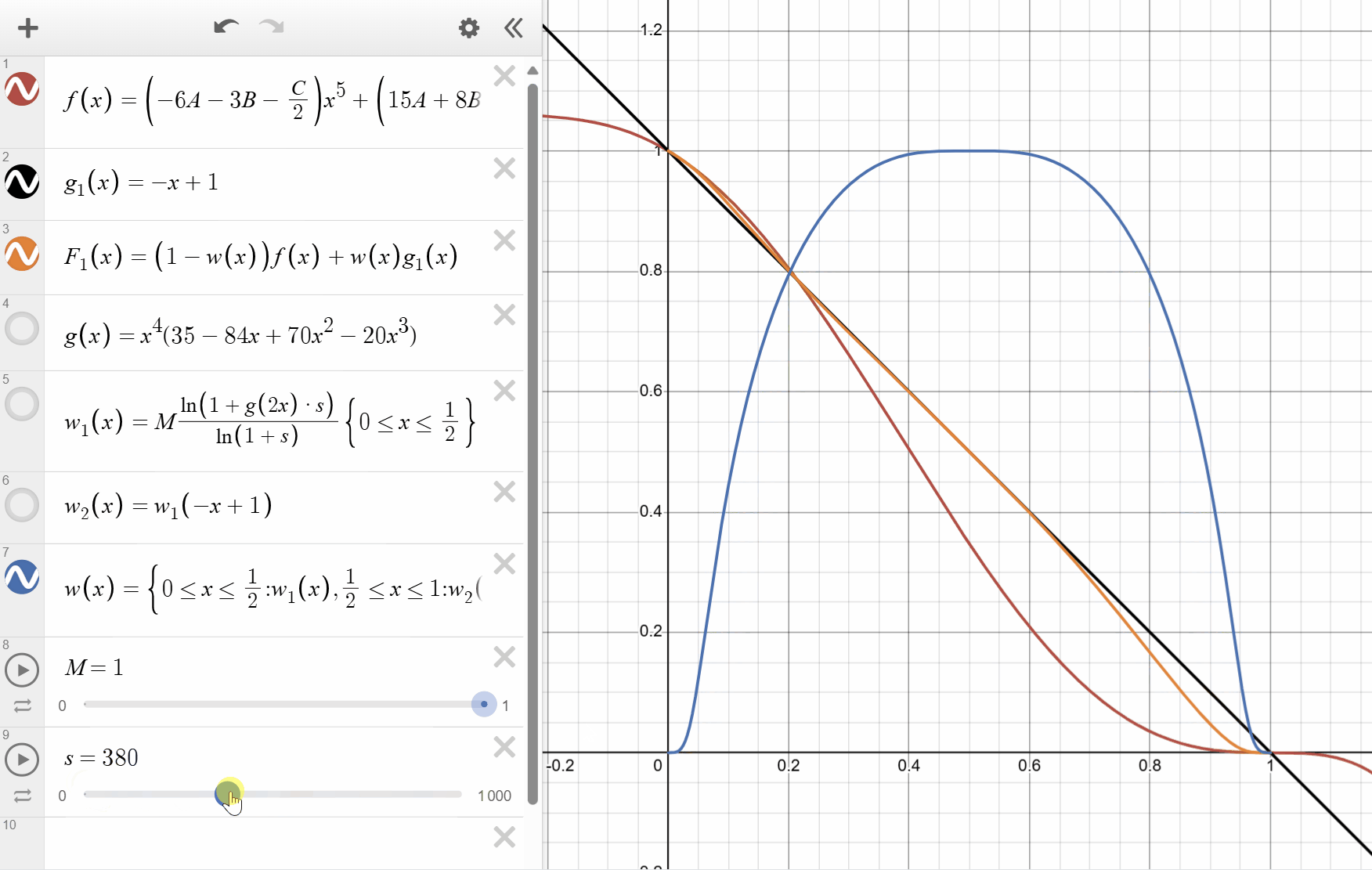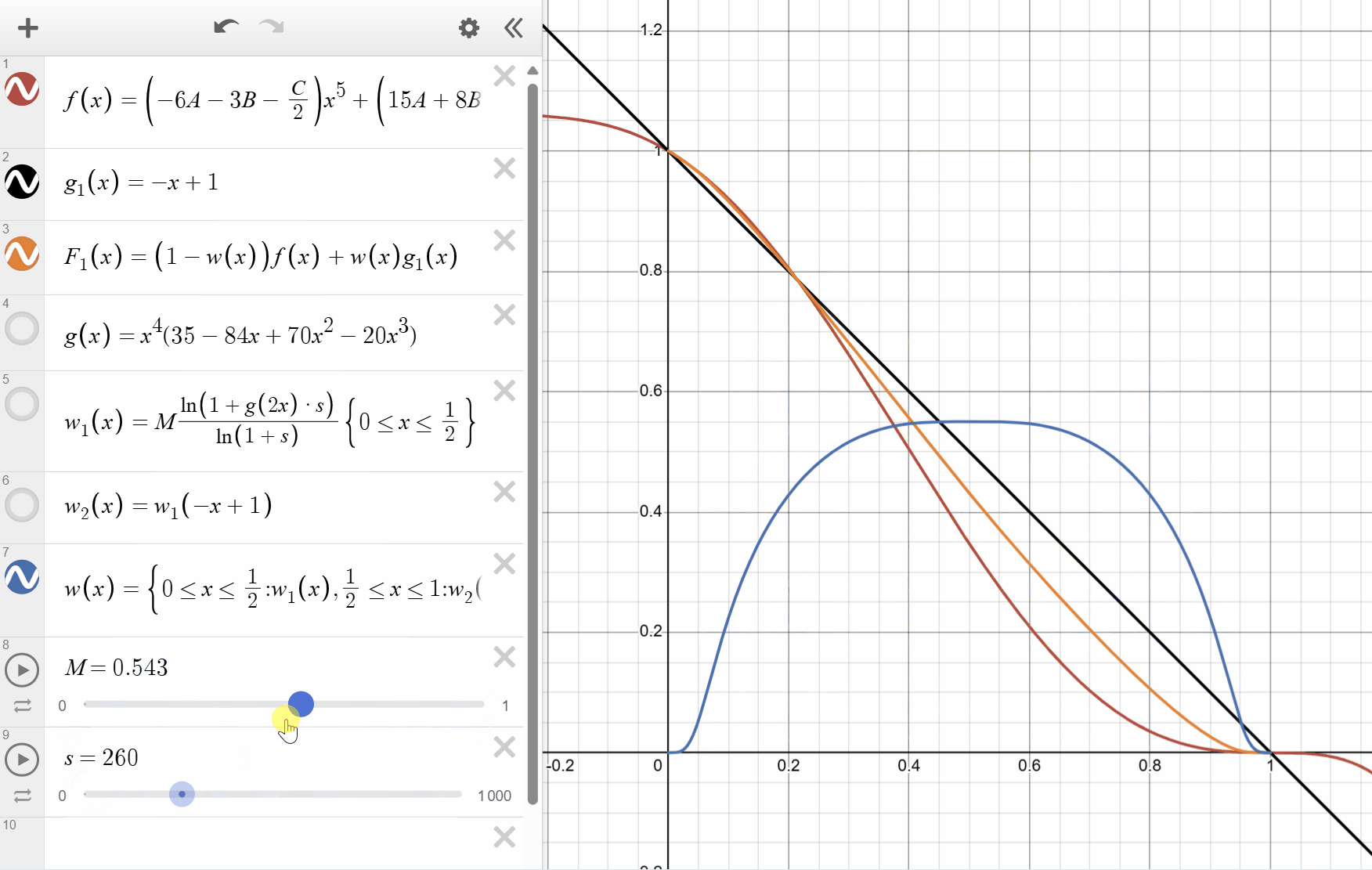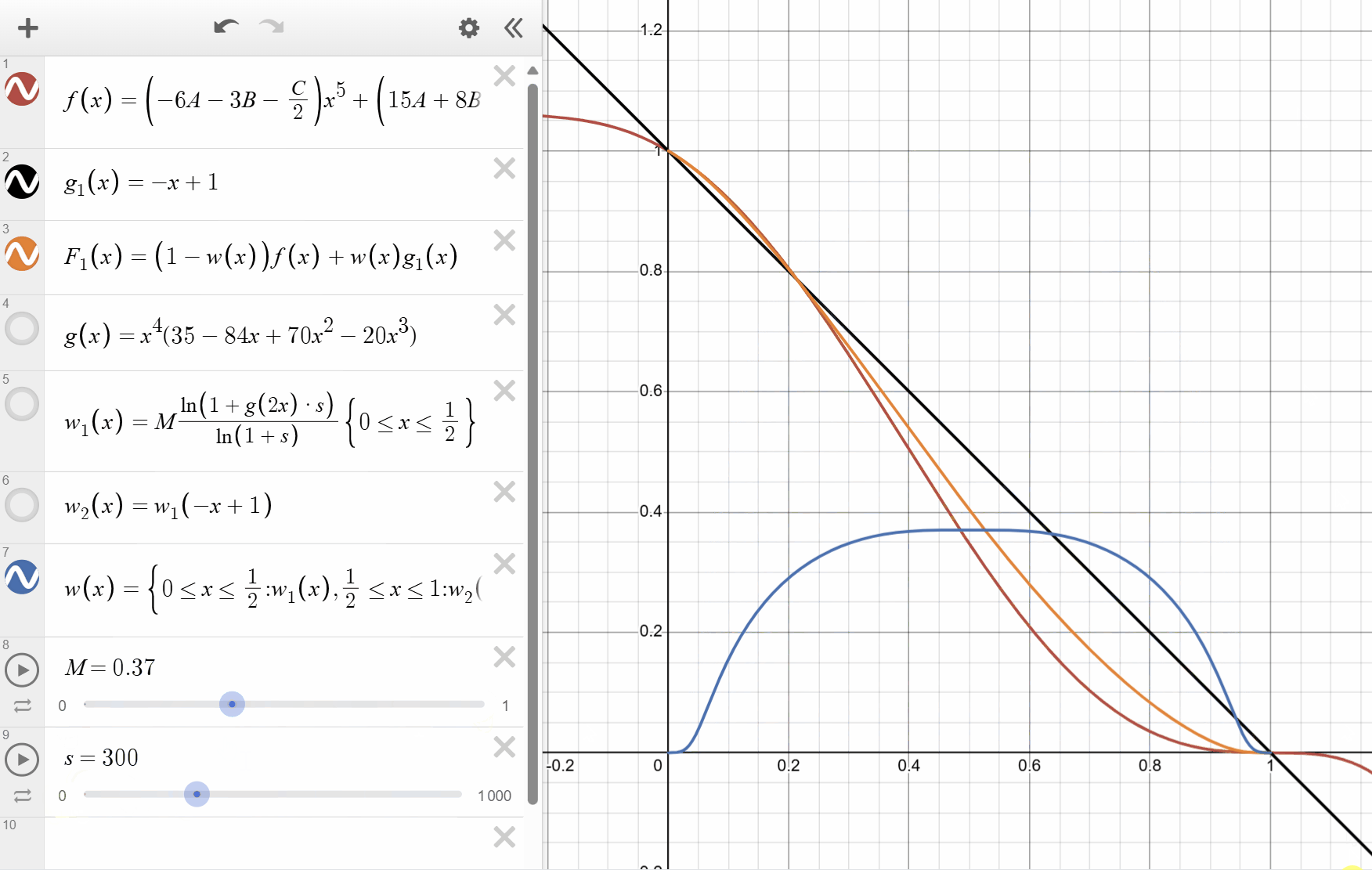
You can see that by tweaking and you can have a full control over the shape of the final blend curve, completely following the original inertialized curve, or the additive curve.

Automatic Blend Time

Sometimes it's tricky to determine a good blend time which creates the most appealing and smooth camera movement. The most important thing about creating a good camera is, the acceleration should never exceed a particular threshold. It's not actually about the velocity: a fast-moving camera at a fixed speed can be very comfortable to players. To this end, we can constrain the maximum amount of acceleration and choose such blend time that the acceleration of will never exceed or .

First, we have the second derivative of :

This is a third-order polynomial which means it has at most two extreme points. One of them is known, , and the other one, as can be calculated, is . To make sure , we must ensure . We can discuss the value of and find the real maximum value of in . But there's a better choice: we can use as an approximation to since for most of the time it holds.

Hence, the problem becomes:

There are two equations to solve:

Their solutions, if exist, are:

We discard the negative part, so the final solution will be:

is our default blend time, say, set to .

Here are showcases demonstrating the auto blend time respectively with max acceleration , and :

:

:

:

The 'Right' Way to Inertialize Rotation for Camera

Seems everything goes perfect so far! Let's have a test. The following figure shows an inertial transition from a third person camera to a orbital camera moving at a fixed speed around the center of the scene.

Wait... the camera rolls during transition, but the start camera and the end camera neither has rolls! That's because we're dealing with the axis angle or quaternion instead of the euler angle. Even if both source and target rotations have no rolls, the axis-angle or quaternion interpolation still has the chance to produce roll.

One way to solve the issue is to simply set the roll to zero, and it looks like this:

Better. But the pitch seems does not seem good, since the pitch, yaw and roll are blended as a whole, and only resetting roll leaves pitch not feeling so natural.

To humans, the most natural way to feel the rotation is through yaw, pitch and roll independently. Though this not might be the best choice for blending mathematically, but it should be the most intuitive interpretation to players.

So, we inertialize yaw, pitch and roll as indepent components and combine them together to the output rotation each frame. But there is one thing to note, the euler angle of yaw, pitch and roll is not closed, and rather it's cyclic. In Unreal, a degree of is equal to for euler angles. That means, when calculating the initial value and initial velocity , we must normalize them before feeding them to compute other coefficients. We normalize yaw to and pitch to . Doing so, we convert a yaw angle from to because this is the shortest angle the transition will go to the target rotation.

The following figure shows the rotation without normalization. You can see the camera rotates multiple cycles.

In the following figure, the transition goes through the shortest path with normalization.

That's exactly what we want for rotation!

Conclusion

The insight to use inertialization for camera transition is very intuitive, but with a little modification to suit our needs for cameras. We revisited the core mathematical formula, the inertialization polynomial, and invented several new techniques allowing us to automatically set the blend time, combine with a pre-defined curve, and create a more visually appealing rotation transition feel. I hope you find it helpful!