Bresenham's
Algorithm是计算机图形学中用于画直线的算法，它只涉及整型数值的乘法和加法，在底层运算上提高了效率。本文介绍Bresenham算法的思路与扩展。
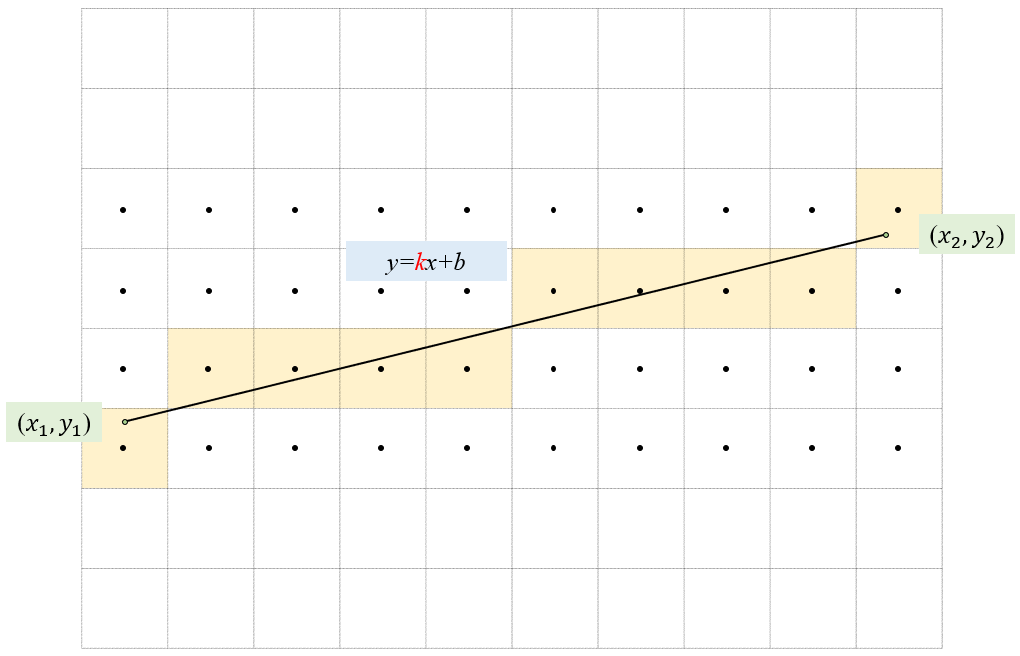
我们用显示器看到的各种图像都是由一个一个像素组成的，比如计算机要在显示器上显示一条线段，那么就要决定哪些像素填色，哪些不填色，如下图所示。下面我们假定像素点坐标为且坐标为整数，所给线段的两端点为，且坐标也为整数。
Naive Algorithm
显然，线段所在的直线的斜率是，直线的方程就能够显式地写出来：，其中。
于是我们可以得到一个非常朴素的算法：从点开始，每次让横坐标加一，即，然后依次把横坐标代入到直线方程中，得到纵坐标，然后去找离它最近的，可以表达为，从而点就是要填色的像素。接下来考虑，重复这个过程，直到。
这个方法如下图所示，注意红色线段和蓝色线段部分是直线上的变化：
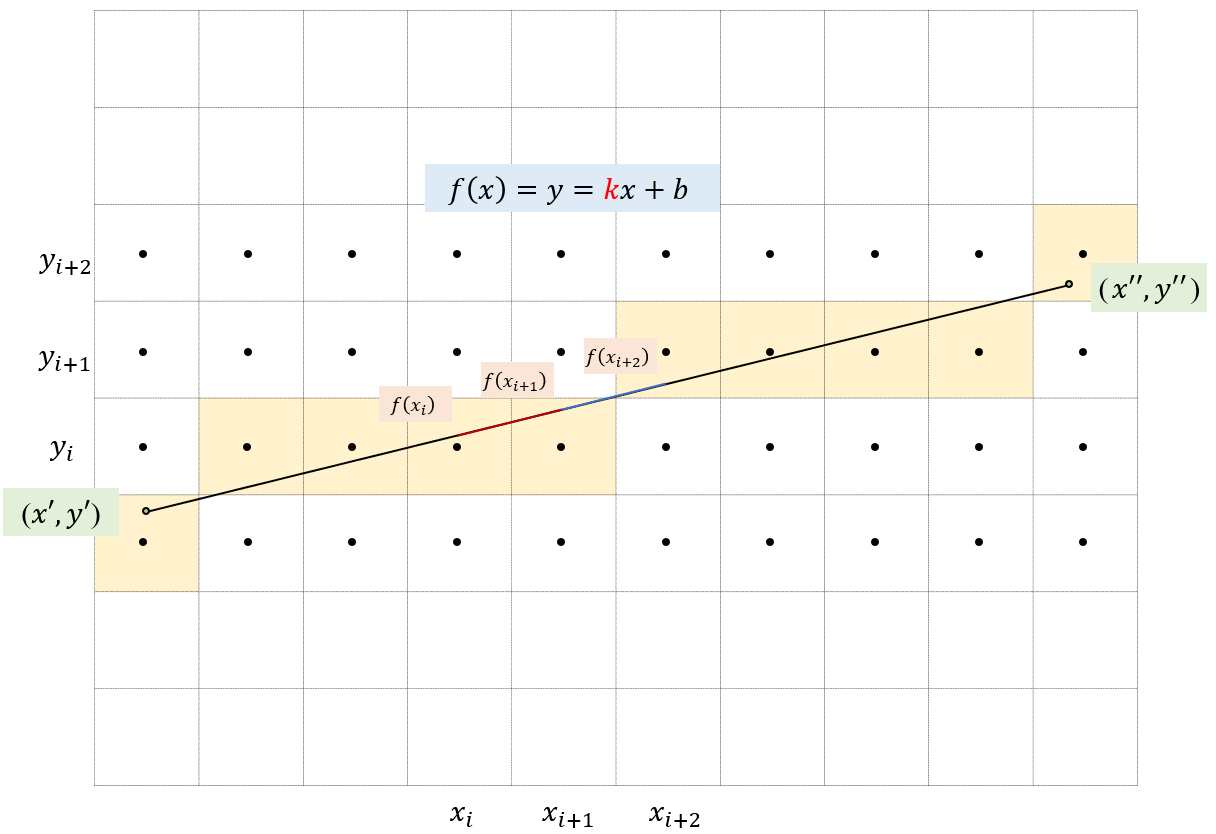给定线段的两点，可以得到它的直线方程，然后依次增大像素点的横坐标，求出对应横坐标的函数值，判断它的纵坐标是什么，得到填充点
当然这个算法可以再高效一点，因为上面在算的时候是用直线方程去算，每次计算都有一个加法和一个乘法，我们可以迭代地去做：。现在，计算就只需要一次加法即可。
这个算法的好处在于，只要直线不是，无论是多少，两个点的位置如何，这个算法都适用。当然，的情况特殊考虑即可，问题不大。
但是这个算法的问题在于，斜率往往是浮点数（即使端点都是整型），而计算机计算浮点数的效率远没有计算整型快，而在图形学中，需要进行大量的即时演算，我们希望能够尽量避免浮点运算。而且，在求时必不可少需要取整，这进一步降低了运算的效率。
Bresenham Algorithm
下面我们介绍Bresenham算法，一种基于Naive算法的改进版本，它不需要使用取整函数，而且大部分的加法与乘法运算都是基于整型，在运算效率上大大提高。下面我们假设直线斜率且，原因及一般的情况我们在下面会介绍。
现在我们仔细观察Naive算法，会发现其计算瓶颈主要由和带来，换句话说，Naive算法假定我们对每一个都要去计算它在直线上的精确位置，而且还要直接计算它离哪个纵坐标更近。
假定我们现在已经着色了点，如下图所示。
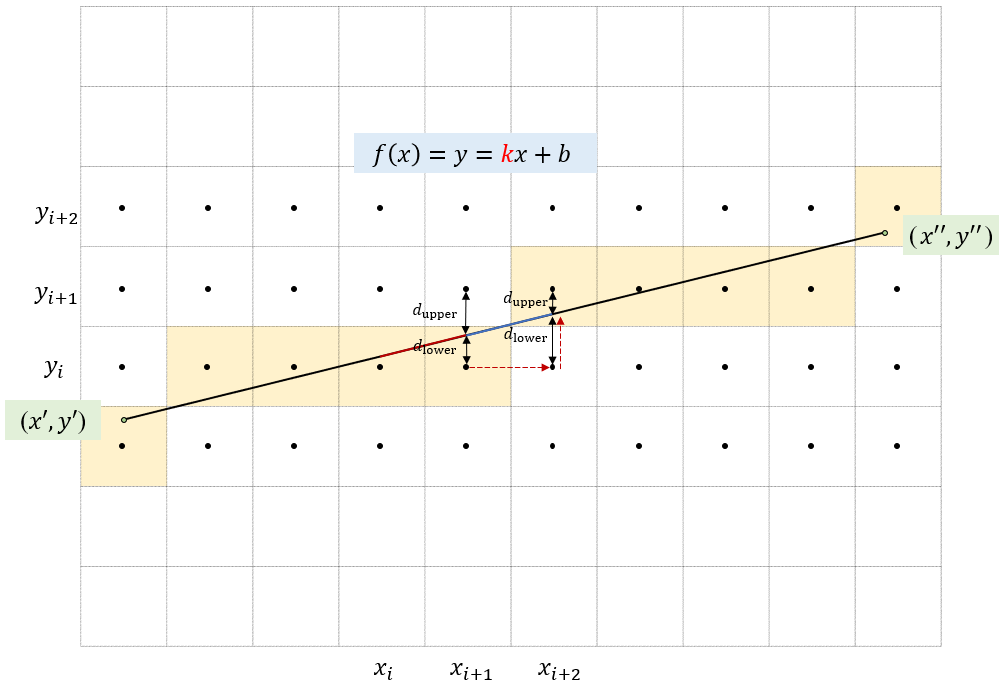Bresenhan算法相比Naive算法的改进之处在于，在求像素纵坐标的时候，不直接用取整函数，而是考虑上下相邻两个像素点与函数值的距离，小的那个才是真正需要着色的，于是就把问题转为了两段距离的大小比较
由于我们的假定，所以下一个要着色的点只能是或者，也就等价于计算和的大小，我们把它们分别记为和。现在对它们做差，就得到：
上面，是与无关的常量。所以，现在我们就只关心的正负如何，但是上式还是有，我们记，于是，代入到上式，就得到了：
由于我们又假设了，所以为正，要判断的符号也就是要判断的符号，此刻我们记。所以，只要判断是大于0还是小于0，就可以判断对横坐标而言，是要选还是为纵坐标了。
现在我们把代入，就得到初始值:
虽然上式已经成功去掉了计算，但是要计算还需要每次都加常数项，而它仍然包含了浮点数，我们还是想要不计算它们。但是我们观察到，都包含常数项，所以我们对它们做差就可以消去常数项，得到:
或者写成下面的递推形式：
现在，已经不用再计算浮点数了。我们前面已经说了，可以用去判断和的关系，然后，就可以把代入上式，计算出了。
所以，当的时候，，等于，此时计算得；当时，，，此时计算得。然后再用去判断，从而可以计算，一直下去，直到。
注意我们的两个前提和，前者保证了每次最多增加1，后者保证了为正。
总结来说，Bresenham算法的流程是： 这里的根据计算结果选择。
下面是一个例子，设给定的两点是，从而，把这些都计算好之后，首先填充这个像素，然后发现，则下一个点的纵坐标还是3，于是填色像素，计算；发现又为正，则下一个像素是，计算；此时发现为负，则向上移动一格，要填充的像素是，再计算；以此类推。
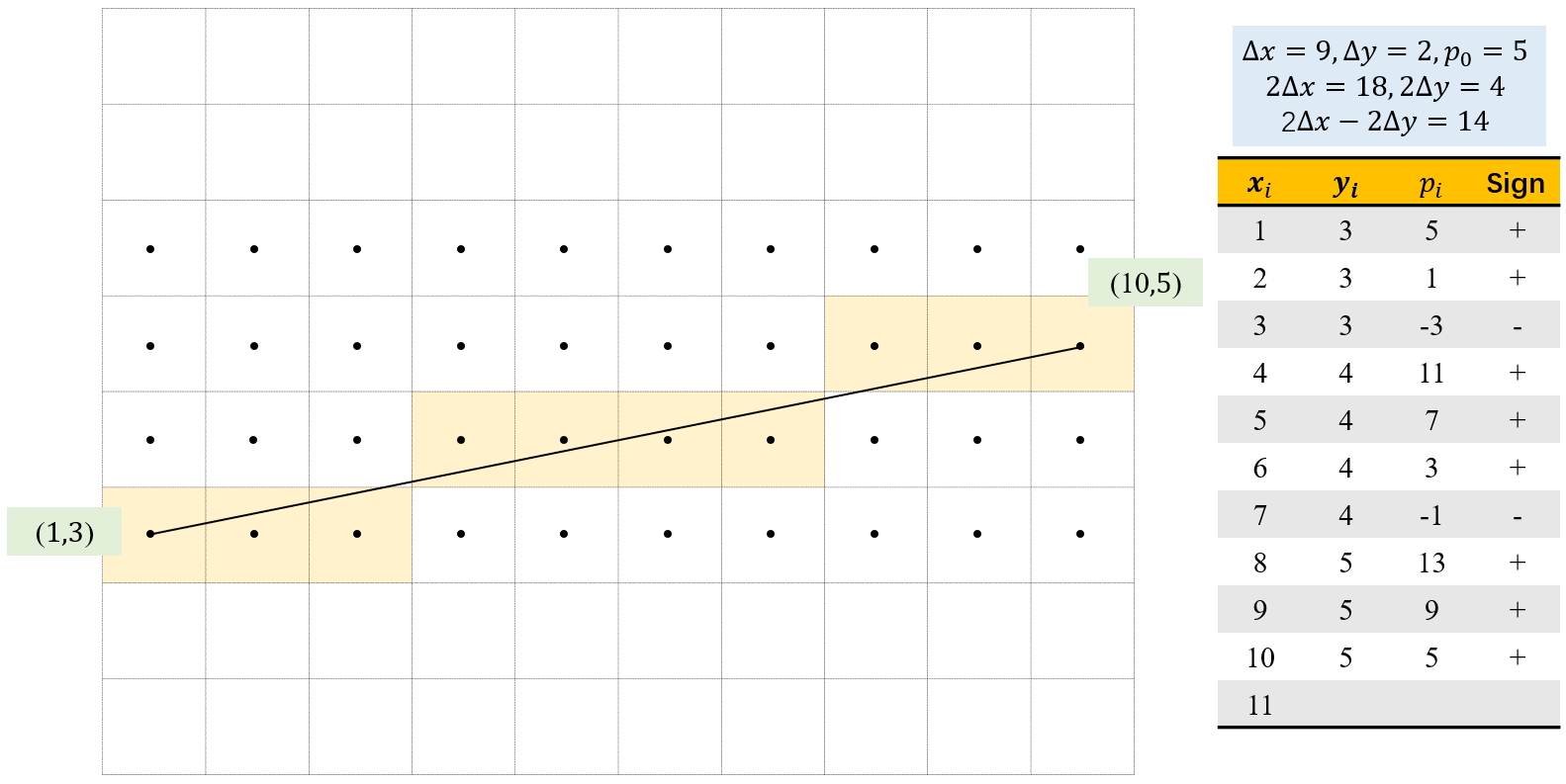一个使用Bresenhan算法画线的实例
由于线段没有方向性，所以我们可以始终将第一个点设为第二个点的左侧，即。那么现在的问题就是要解决和的问题了。可以发现，不同的其实对应了平面的不同区域，根据对角线与坐标轴可以分为四个区域。现在，只需要对和对应的线段进行对称操作，就可以转换为的情况。在求得所有填色的像素之后，再把这些像素对称回去即可。